Eu gostaria muito de poder intitular esse texto como “Tensão Real, Estricção, Ductilidade e o Módulo de Poisson”, mas ficaria feio na capa, ficou esse tema mesmo. No entanto, esteja ciente, incauto leitor, que os conceitos do tema desejado serão tratados. Portanto, adianto que os textos anteriores a este são de suma importância para a compreensão. Tanto que, mais uma vez, vamos começar observando nosso plano retirado do grão de um corpo sólido, como é mostrado na Figura 1.

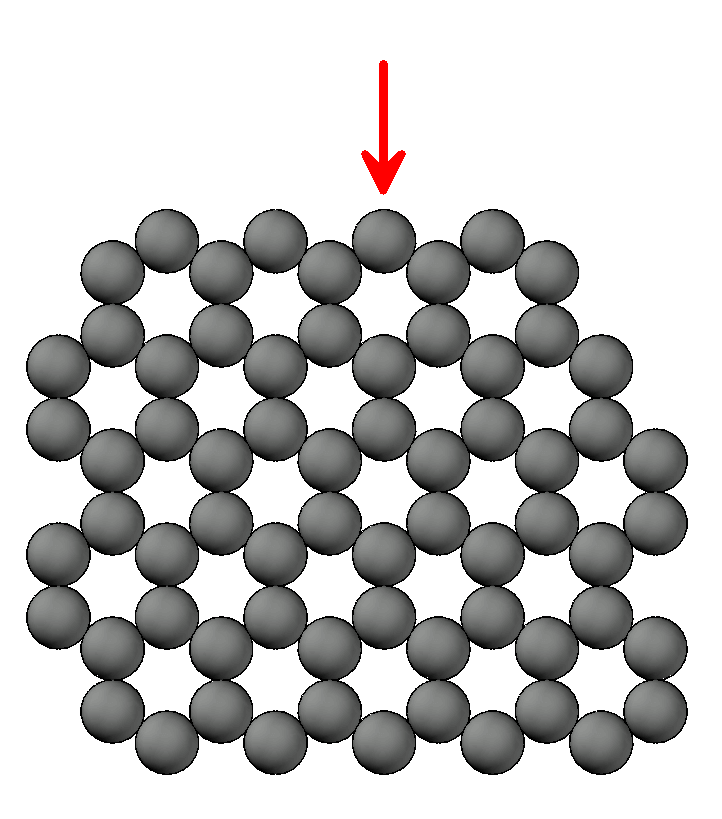
Figura 1 – Plano de Grão

Para a explicação do primeiro conceito, utilizaremos um grão perfeito. Sem defeitos pontuais, lineares ou planares. Lembremos que tanto as moléculas de um material quanto seus átomos possuem uma força de ligação e uma distância de equilíbrio. Qualquer perturbação na distância de equilíbrio causará uma tendência de alteração da posição desses átomos. Começaremos deslocando um átomo em apenas uma das estruturas hexagonais repetitivas desse grão (plano de célula unitária), como mostra a figura 2. Mas, como é fácil intuir, para mover um átomo é preciso aplicar uma força sobre ele. Guardemos esse conceito para futuros textos: Deslocamentos exigem carregamentos.

Ao aplicarmos uma carga, gerando assim um deslocamento de um átomo de um grão, as forças de ligação entre os átomos agirão para manter o material unido. Assim, a força é transmitida e os dois átomos se deslocarão a fim de manter a mesma distância interatômica. Ao deslocarem-se, não existem as fronteiras dos outros dois átomos para manter a distância que mantinha o hexágono perfeito. Os átomos se aproximam alterando o ângulo inicial do hexágono, assim, também, mudam o ângulo formado entre a vertical e os próximos dois átomos a serem deslocados, alterando seus deslocamentos.

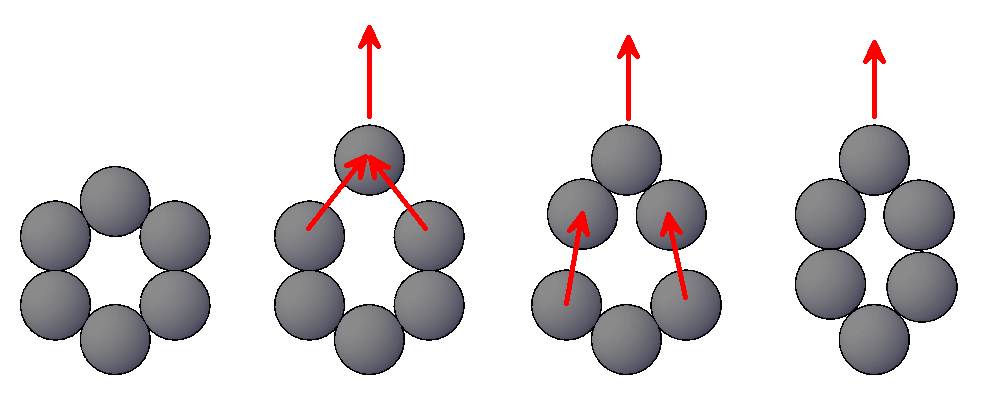
Figura 2 – Deslocamento entre átomos de um grão.

Ampliando o conceito, há de se lembrar que ocorre a dissipação das tensões de forma amortizada como foi visto no texto “O princípio de Saint-Vernant”. Onde o deslocamento era causado por uma força de compressão. Esse mesmo conceito aplica-se à tração, que será utilizada aqui para explicar outros conceitos. Utilizando a compressão neste momento e se valendo daquilo que foi explicado na figura 2, é compreensível que, se uma força de tração altera o hexágono original como mostra a Figura 3ª, então uma força de compressão causará a alteração mostrada na figura 3b.

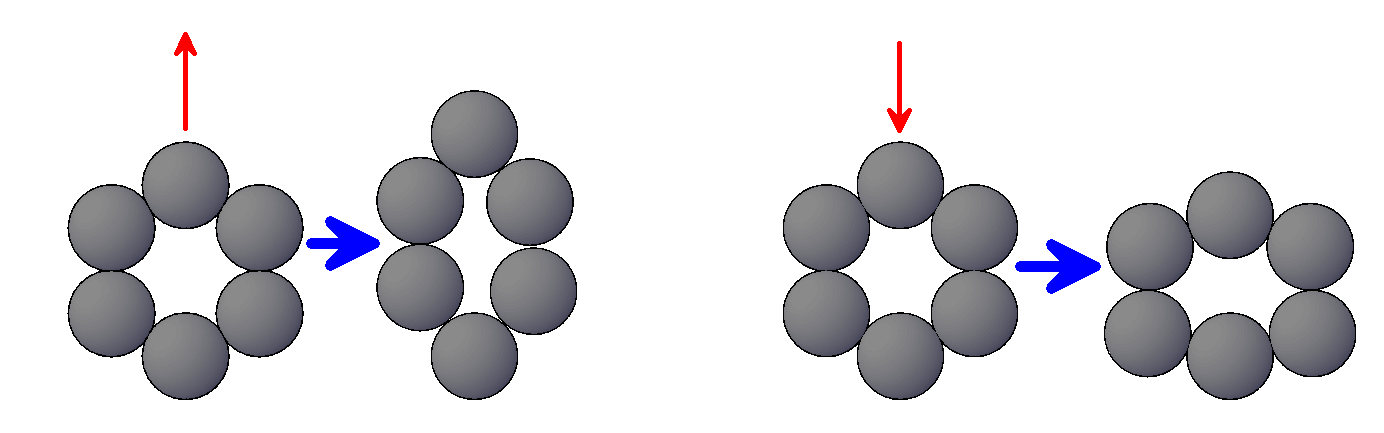
Figura 3 – Deformações causadas pela tração e compressão em um plano de célula unitária.

Como já foi explicado no blog, uma célula unitária é a menor estrutura de repetição de um corpo sólido. Se essa célula se repete, então é fácil perceber que, essa deformação ocorrerá em todo o corpo. Utilizando o plano de grão é fácil perceber que, como o deslocamento ocorrerá em mais átomos quanto mais embaixo estivermos neste plano-exemplo, então as mudanças dimensionais transversais á carga serão mais sensíveis quanto mais distante estivermos da aplicação de carga. Já nos deslocamentos longitudinais à carga, a sensibilidade será maior quanto mais próximos estivermos da carga. Isso é possível deduzir observando a figura 4 que mostra a distribuição das cargas de compressão no plano.

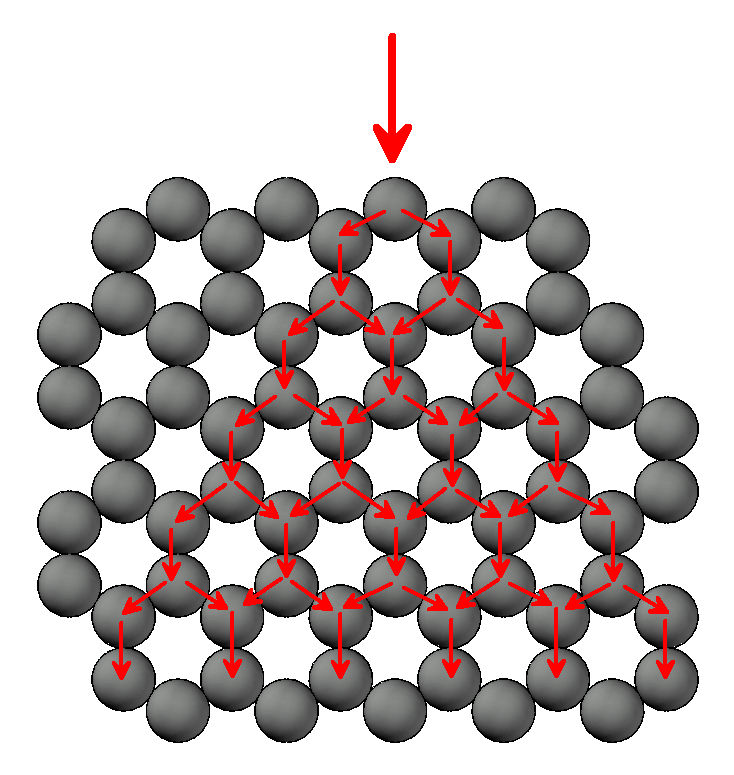
Figura 4 – Distribuição das cargas de compressão em um plano de grão.

Portanto, ocorrerá a deformação do plano reduzindo sua altura e aumentando sua largura, como mostra a figura 3b. expandindo o conceito, poderemos observar esse efeito na figura 5. Esse efeito explica-se basicamente por estarmos deslocando massa. E como os átomos não podem se penetrar mutuamente, ocorre um rearranjo das posições de seus átomos que alteram as dimensões transversais e longitudinais. Para compressão, redução da altura e aumento da largura como mostra a Figura 5. Para a tração, aumento da altura e redução da largura como mostra a figura 6.

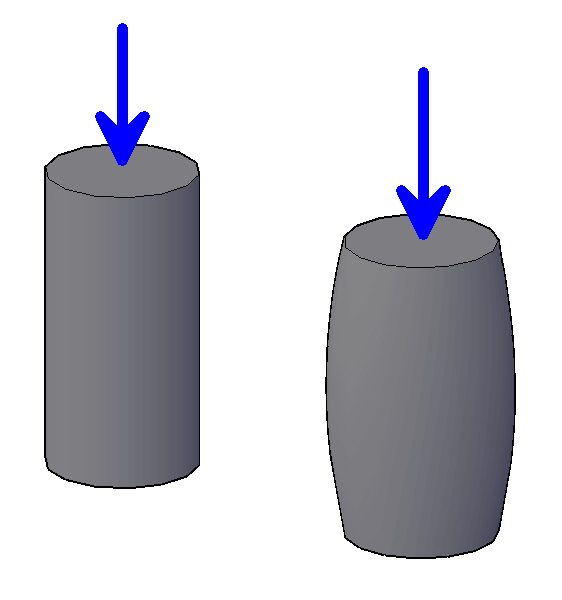
Figura 5 – Mudança nas dimensões de um corpo de prova cilíndrico devido à compressão

Figura 6 – Mudança nas dimensões de um corpo de prova cilíndrico devido à tração

Assim sendo, tomando a compressão como exemplo, e lembrando os conceitos apresentados no texto “Tensão e Deformação”, podemos escrever as deformações específicas longitudinais e transversais conforme as equações 1 e 2 baseando suas relações na figura 7.

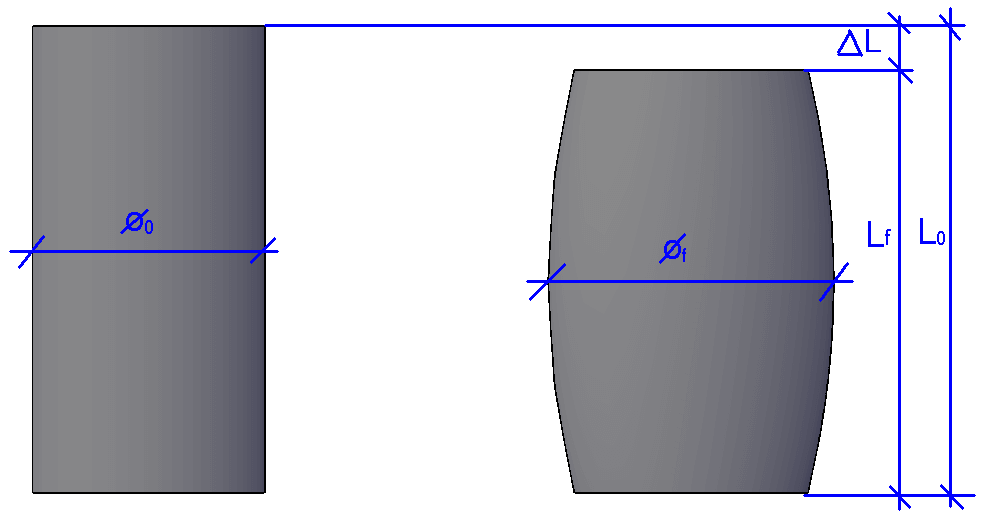
Figura 7 – Relações dimensionais de um corpo de prova cilíndrico comprimido

A fim de generalizar o conceito, entenda que tanto para as direções x e y podemos ter deformações diferentes. Por exemplo, se um corpo de prova for de base retangular, então suas dimensões e, x e em y serão diferentes e teremos εx eεy com valores não-coincidentes, como ocorreu no nosso exemplo com o corpo de prova cilíndrico que culmina numa coincidência dos valores.

A partir das equações 1 e 2 (lembrando que é necessário generalizar a equação 2 para corpos de dimensões diferentes), Siméon Denis Poisson, em 1800, na França, postulou o Coeficiente de Poisson. Que nada mais é do que relacionar a razão entre as deformações ocorridas transversalmente com as deformações ocorridas longitudinalmente como consta na equação 3. Como, o cientista francês estudou gases à compressão, não corpos rígidos (contudo o conceito pôde ser expandido), à compressão, o comprimento final é menor do que o comprimento inicial, o que culmina em um valor negativo da deformação específica na direção z. Da mesma forma, na tração, a largura final é menor do que a largura inicial tornando a deformação específica negativa nas direções x e y. Como o coeficiente precisa ter valor positivo para ter sentido físico, isso foi corrigido na equação 3 adicionando um sinal negativo antes da relação de Poisson.

Esse conceito interfere em diversas análises de Engenharia e o caso da tensão real, que será mostrada no próximo texto e em áreas de análises por Elementos Finitos, Teoria da Elasticidade, teorias da plasticidade, Estados bi e triaxiais de tensão entre outras. Cada conceito até aqui apresentado nos permite avançar em áreas diversas e tudo o que foi visto apresenta a necessidade de estudos, outros, como o estudo da ciência dos materiais, para melhor compreensão da mecânica das estruturas e até mesmo do seu projeto e detalhes de suas construções. Como dito, a função pensada para este blog é a apresentação através de uma ótica menos densa dos conceitos básicos a intermediários da mecânica das estruturas. Assim seguiremos.