Chegou a hora de explicar pra quê servem os estudos sobre tensões e deformações. Pois, bem. Tudo isso serve como base para estudos mais aplicados à realidade. Inicialmente precisamos entender os ensaios, a máquina que utilizamos e por que precisamos saber esse parâmetro. Antes disso tudo, no entanto, preciso lembrar que este blog não possui o intuito de ensinar qualquer pessoa a projetar. Mas, a compreender as nuances dos conceitos que utilizamos nos cálculos dos diversos parâmetros estruturais.

Vos apresento a prensa. Mostrada na Figura 1, uma prensa computadorizada da marca EMIC. Para ensaios de tração. Na figura 2, mostramos um corpo de prova normatizado utilizado para ensaio de tração no aço sendo fabricado a partir de uma barra de aço CA-50 e na figura 3, o mesmo corpo de prova sendo tracionado na prensa. A figura 4 mostra a mudança de comprimento (Δl) do corpo de prova antes e depois de sua ruptura. A figura 5 mostra o mesmo ensaio sendo realizado em uma barra de aço CA-50 no formato de fábrica.

Figura 1 - Prensa para tração no aço

Figura 2 - Confecção de corpos de prova para ensaio de tração no aço

Figura 3 - Ensaio de tração no aço com corpo de prova normatizado

Figura 4 - Comparação de corpo de prova de aço íntegro e rompido

Figura 5 - Ensaio de tração no aço em barra

Com uma pequena troca de aparelho (substituição da garra por rótulas), é possível utilizar a mesma prensa para ensaios de compressão em corpos de prova de concreto, como mostra a figura 6.

Figura 6 - Prensa para ensaio de compressão no concreto e tração no aço (prensa universal)

Com isso, podemos apresentar-lhes as medições feitas pela prensa e, posteriormente, tratar os valores, inserir em gráficos e interpretar o comportamento dos mesmos. Convenientemente, os dados são apresentados conforme as figuras 7 e 8 devido aos termos utilizados na equação final do texto publicado nesse BLOG intitulado “Tensões e Deformações”.

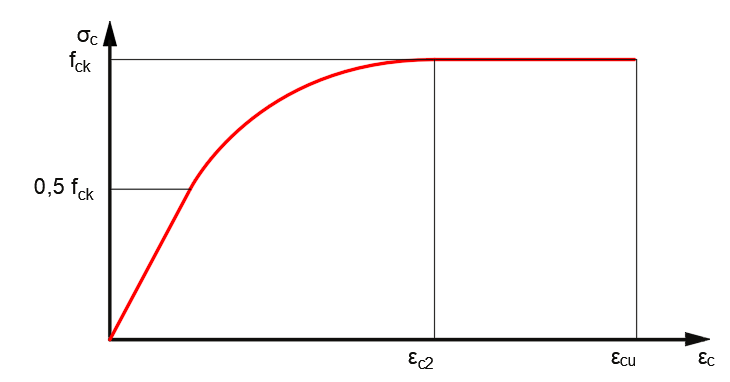
Figura 7 - Diagrama tensão x deformação do concreto

Figura 8 - Diagrama tensão x deformação do aço

O que reparamos normalmente é a pouca disponibilidade de material que explique na prática o uso e importância desses diagramas. Pois, a proposta desse texto parte desse propósito. E a importância da compreensão desses diagramas e suas aplicações é extrema. É a partir deles que começaremos a compreender a mecânica estrutural do Concreto Armado e das Estruturas Metálicas.

Vamos começar observando a figura 9. Ela apresenta o conceito de Energia de Deformação Elástica. A parte elástica da deformação é exatamente o único trecho dos diagramas que tensão-deformação que obedece a lei de Hooke aprendida no último texto (Tensão e Deformação). Após esse trecho, os diagramas perdem a proporção linear de proporcionalidade e entram em um estado plástico de deformação. Conceituando de forma simples: Dentro da região elástica o material não está danificado e recupera sua forma original algum tempo após as forças cessarem, exatamente como uma mola, como foi mostrado no texto anterior. Por isso foi utilizada a analogia de mola. A figura 10 mostra a área elástica dos diagramas do aço e concreto

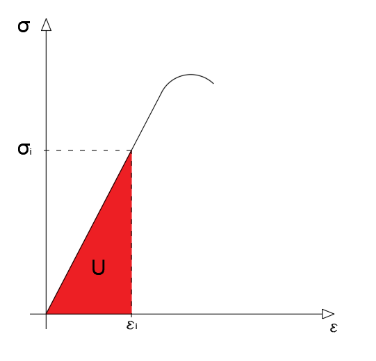
Figura 9 - Apresentação da Energia de deformação elástica

Figura 10 - Identificação da região elástica dos diagramas tensão x deformação do aço e concreto

Para perderem a proporcionalidade direta entre tensão e deformação, os materiais precisam se alterar. Essas alterações causam efeitos diferentes dependendo do material. Essas mudanças serão explicadas no próximo texto deste blog. Por hora vamos nos ater a explicar essa propriedade que recebeu o nome de “Elastoplasticidade”. Que é descrito por Neto (2008) como o comportamento de materiais que depois de um ciclo de carregamentos apresentam deformações permanentes.

Para explicar o comportamento do gráfico utilizaremos o aço e os conceitos aprendidos no texto anterior. Observando a figura 11, as forças F0, F1, F2, F3 e F4 serão forças medidas de valores quaisquer iniciando em F0 = 0 kN e evoluindo convenientemente. As prensas comerciais são controladas principalmente por velocidade de deslocamentos e medem a força necessária para causar aquele deslocamento. Então, não necessariamente as forças são crescentes. Conhecida a área da barra de aço é possível obter as tensões (σ) para cada força e conhecido o comprimento inicial indeformado (referente a F0) e medidos os alongamentos causados pelas demais forças, conseguimos obter suas deformações específicas (ε), que são as variáveis contidas nos gráficos.

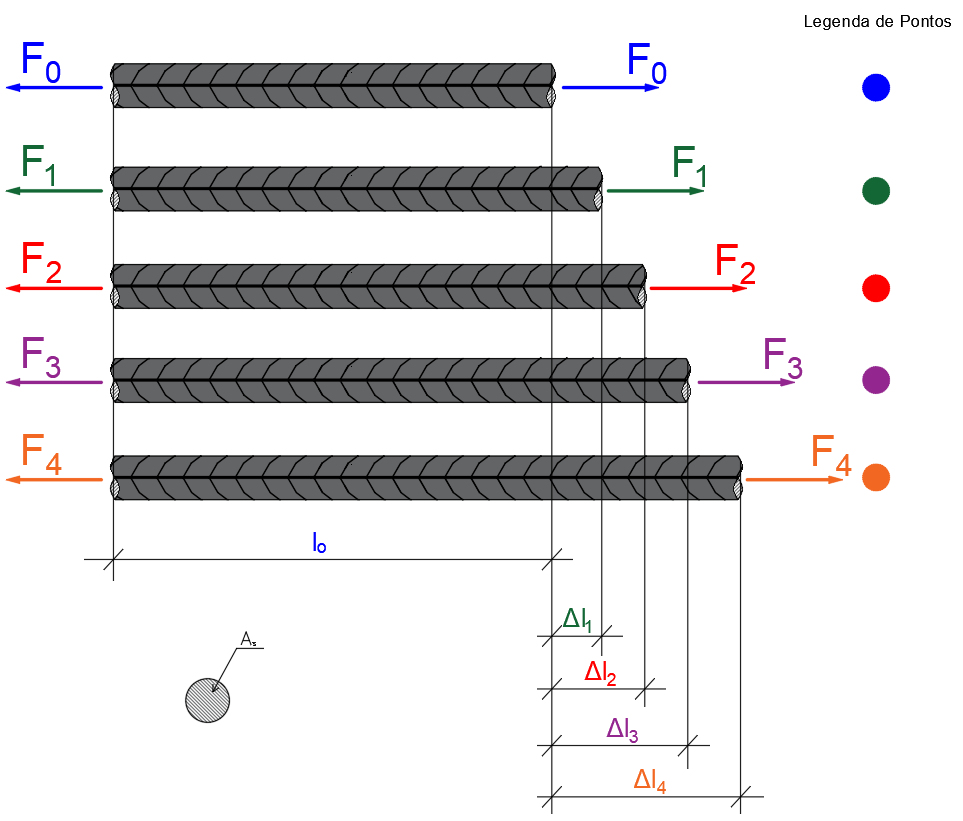
Figura 11 - Níveis de tração do aço exemplificado

Posicionando no gráfico da figura 8, os pontos da figura 11, montamos a figura 12, onde é possível verificar sua posição e o estado da barra nesse ponto. O ponto azul é o indeslocado com força zerada. O ponto verde ainda está na região elástica, ou seja,  caso cesse-se a força, ele (o material) retornará ao ponto azul. O ponto vermelho já atingiu o escoamento. Então, esse deslocamento não retornará. Mas também não é de todo perdido. O material tem uma taxa de retorno, mas fica com uma deformação residual (Δlres) como mostra a figura 13.

O ponto roxo apresenta um material encruado. O encruamento é a propriedade impressa a um material por tratamento a frio para ganho de resistência. Ele possui retorno de parte da deformação sofrida ao cessar da carga assim como o ponto vermelho, como mostrou a figura 13. O caminho desse retorno é o mesmo caminho percorrido pelo ponto ao reaparecerem as cargas no material. No entanto o ponto vermelho não representa um material encruado por não ter sofrido ganho de resistência.

Já o ponto laranja representa um material que já atingiu sua resistência máxima e está em vias de colapso. Nesse estado acontece um fenômeno chamado de estricção que é a perda de seção (diâmetro e, consequentemente, área). O corpo de prova da figura 4 mostra esse fenômeno.

Figura 12 - Posicionamento dos níveis de tração no diagrama

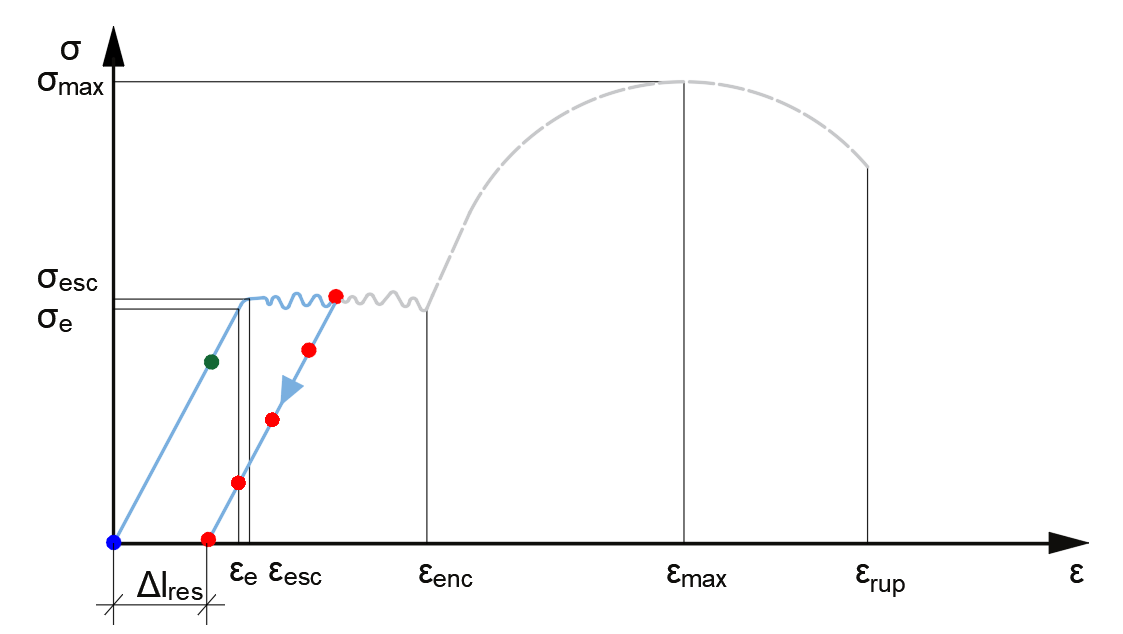
Figura 13 - exemplo de destracionamento de aço escoado

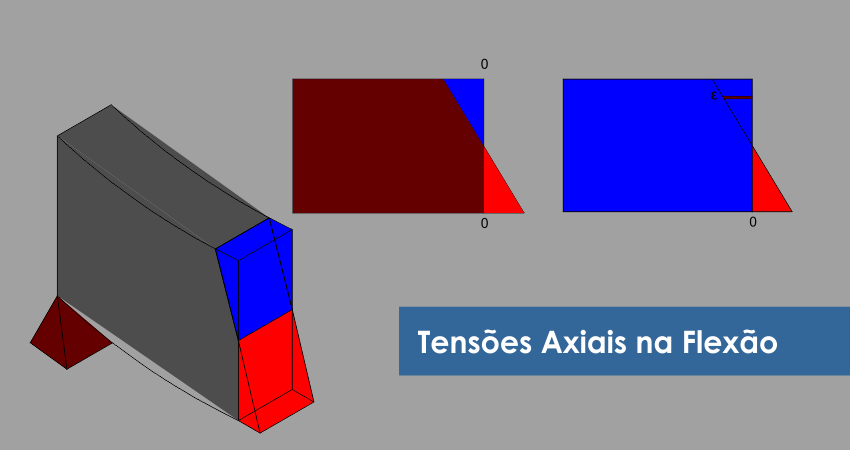
O mesmo efeito descrito para o aço acontece no concreto, mas em um diagrama onde não ocorre ganho de resistência após o escoamento (Figura 1). Então surge a nossa pergunta: Por que eu preciso conhecer os diagramas e saber interpretá-los? Simples. Porque eles aparecem nas estruturas. Mentalize uma viga e imagine que ela seja biapoiada com carregamento qualquer no meio de seu vão. O momento fletor vai obrigar que o concreto na parte superior se encolha enquanto o aço na parte inferior se alongue como mostra a figura 14.

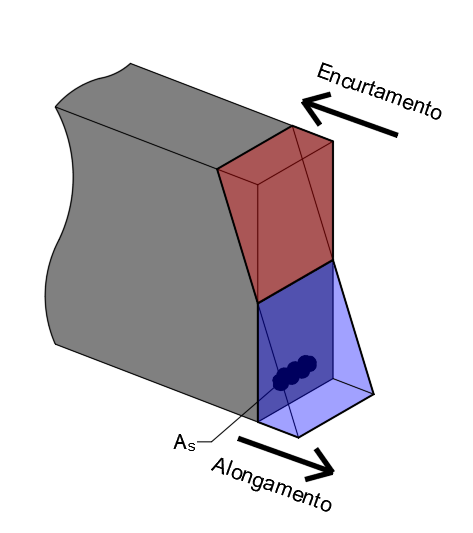
Figura 14 - Seção de viga deformada

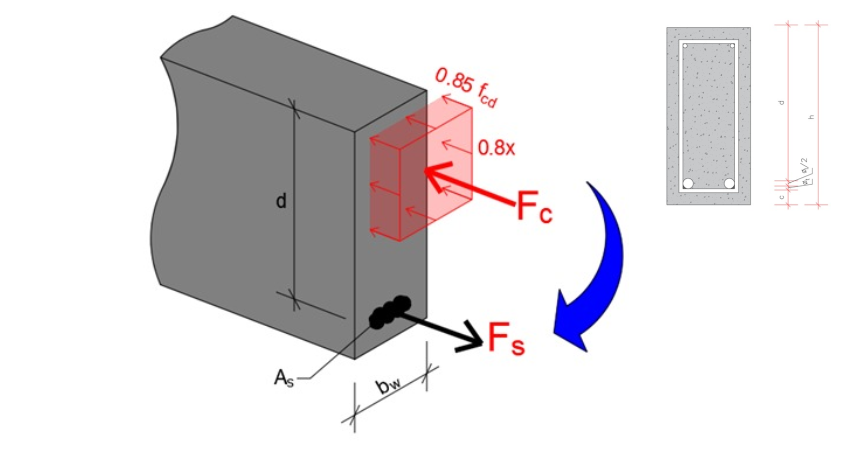
Reparem que o concreto é gradualmente comprimido da linha neutra pra cima enquanto o aço possui apenas um comprimento de alongamento. Dessa forma, cada lamela do concreto possui um encurtamento e, portanto está submetido a uma força diferente (Lembrem do texto anterior. Quanto mais força, mais alongamento. Tensão é diretamente proporcional à deformação) Portanto, o diagrama do concreto aparece por inteiro acima da linha neutra, na seção, enquanto o aço possui apenas uma força aplicada por sofrer alongamento por igual em sua seção, então funciona exatamente como mostra a figura 11 e 12 onde a barra, na seção, ocupa apenas um ponto do diagrama, como mostra a figura 15. Para efeitos de cálculo, a tensão no concreto pode ser acumulada em uma força Fc concentrada no centro de gravidade do diagrama. Mas, isso é um assunto pra uma próxima publicação;

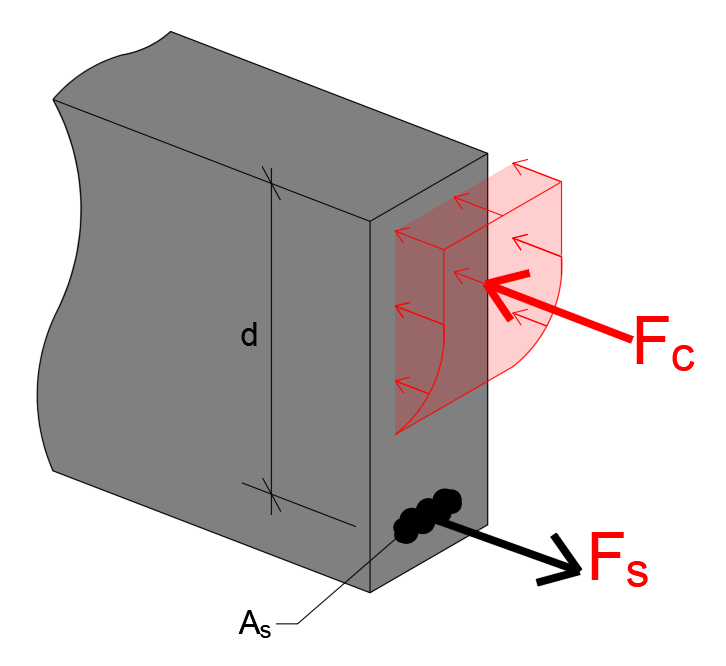
Figura 15 - Representação das tensões e forças em uma seção de viga deformada

A NBR 6118/2014 permite a utilização de diagramas simplificados para o aço e o concreto. Manteremos esse assunto em mente para uma futura próxima leitura.

REFERÊNCIAS

Neto, E. A. S., Perić, D., and Owen, D. R. J. Computational Methods for Plasticity: Theory and Applications. John Wiley & Sons, 2008.