Como primeiro capítulo deste BLOG pensei em apresentar-lhes um ou dois mecanismos que introduzem a idéia da mecânica estrutural. Mas, como o acadêmico que a vida me propiciou ser, preferi inferir conceitos mais iniciais e contundentes para que entendamos de verdade qual conteúdo será abordado e entendermos as limitações que esse veículo manterá.
Não almejo ensinar dimensionamento das estruturas, mas, sim, explicar seu funcionamento e o caminho pelo qual os pesquisadores/cientistas e os códigos normativos chegaram ao equacionamento que dimensiona e verifica as questões estruturais. O objetivo é que, durante as explicações dadas sejam comentados pontos de interferência desse estudo nas diversas áreas da engenharia. Por exemplo: Ao compreendermos o cálculo dos deslocamentos verticais em vigas (através da compreensão das teorias de vigas de Navier ou Thimoshenko, adicionando o entendimento da Inércia Equivalente de Branson), entender como as cerâmicas dos pavimentos desplacam e as janelas “empenam” nos pavimentos com flecha excessiva. Assim, mostramos como a Mecânica das Estruturas se apresenta como ferramenta para elaboração de laudos de Patologia das Construções.
É importante, então saber o que realmente é a Mecânica das Estruturas. Primeiro, observe a Figura 1. Há de se lembrar que foi dispensada a colocação da química como base da Engenharia Civil devido ao enfoque do artigo ser a área das estruturas desta mesma engenharia.
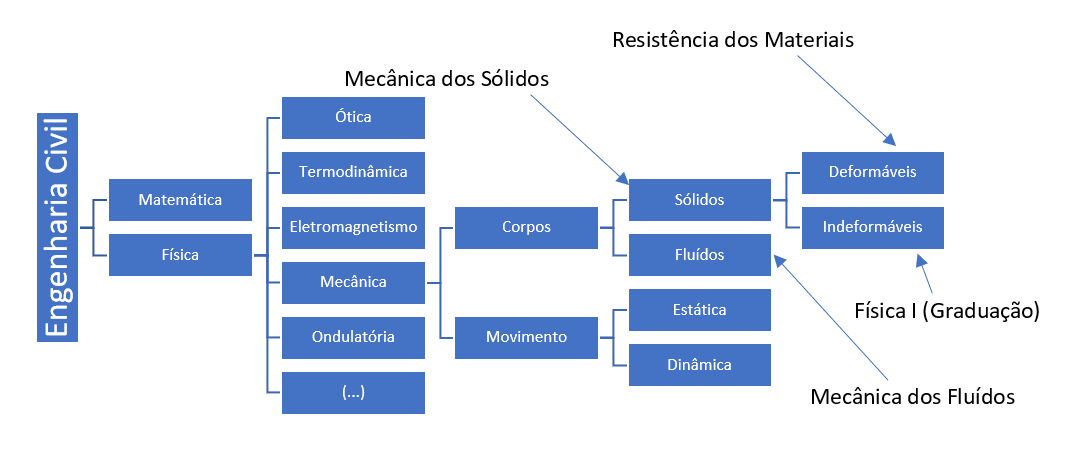
Figura 1 - Organograma da Mecânica das Estruturas
Podemos afirmar que a Mecânica das Estruturas é, primeiramente, uma área da física (Mecânica), que dentre todas as outras áreas, é a que pode utilizada para o cálculo das nossas estruturas compostas pelos sólidos deformáveis e estáticos. Retraindo o conceito da Mecânica dos Sólidos Estáticos e Deformáveis, nomeamos de Mecânica das Estruturas. Tal que, como ponto de partida da Mecânica das Estruturas, temos as disciplinas de Física I, Mecânica dos Sólidos e a Resistência dos Materiais.
As palavras contidas neste conceito (Mecânica dos Sólidos Estáticos Deformáveis) apresentam as primeiras idéias utilizadas nos primeiros cálculos que fazemos na faculdade. Hoje vamos fazer a análise da palavra “Estático” que constitui o primeiro conceito a ser entendido. Uma busca rápida no Google nos retorna o seguinte resultado mostrado na Figura 2.

Figura 2 - Significado da palavra “Estático”
Parado/sem movimento nos obriga a dizer que é algo que não sai do lugar. Algo cuja posição inicial é exatamente igual a posição final. Ou seja, verifica-se que não ocorra a situação mostrada na Figura 3 e sim o que mostra a Figura 4.
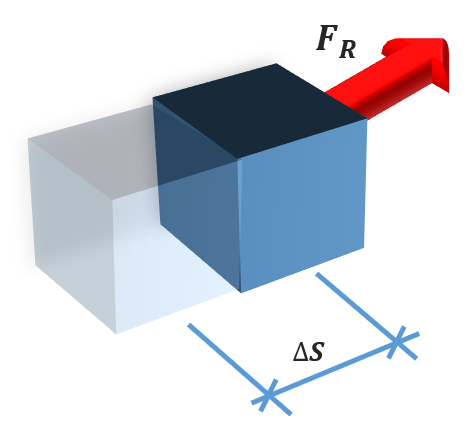
Figura 3 - Deslocamento do corpo
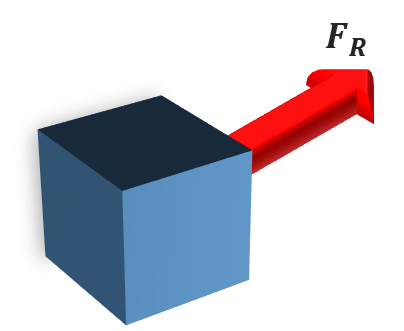
Figura 4 - Deslocamento nulo
|
|
|
Eq. 1. |
Sendo assim, sabendo que a velocidade média é a variação da posição em um certo intervalo de tempo, e substituindo o valor da variação de espaço.
|
|
|
Eq. 2. |
|
|
|
Eq. 3. |
|
|
|
|
E conhecida a equação de aceleração como a variação da velocidade em um certo intervalo de tempo, fazendo a devida substituição dos valores conhecidos.
|
|
|
Eq. 4. |
|
|
|
Eq. 5. |
|
|
|
|
Em se tratando de um ponto acionado por um conjunto de forças, temos uma aceleração resultante e uma força resultante. Tomado que esse ponto precisa estar estático, e a sua aceleração, como provado, deve resultar em zero. Conhecida a equação da força.
|
|
|
Eq. 6. |
|
|
|
Eq. 7. |
|
|
|
Eq. 8. |
|
|
|
|
Dito isso, temos a Equação 8 como a Primeiro Princípio da Estática.
O segundo princípio consiste em garantir que todos os pontos deste corpo estarão em repouso um em relação ao outro. A diferença é que o primeiro princípio garante que a posição inicial do centro de gravidade deste corpo estará em repouso. Enquanto o segundo garante que todos os outros pontos também estarão.
Assim, se o centro de gravidade de um corpo está em repouso, a única forma de haver movimentação dos demais pontos deste corpo, é por rotação entorno do centro de gravidade. Logo, como espera-se que não haja rotação, acelerada ou não, impõe-se que a soma dos momentos seja zero. Sabendo que o somatório dos momentos é exatamente igual ao somatório das forças vezes a distância do ponto de aplicação dessas forças até o centro de gravidade. A Figura 5 mostra esse momento.
|
|
|
Eq. 9. |
|
|
|
Eq. 10. |
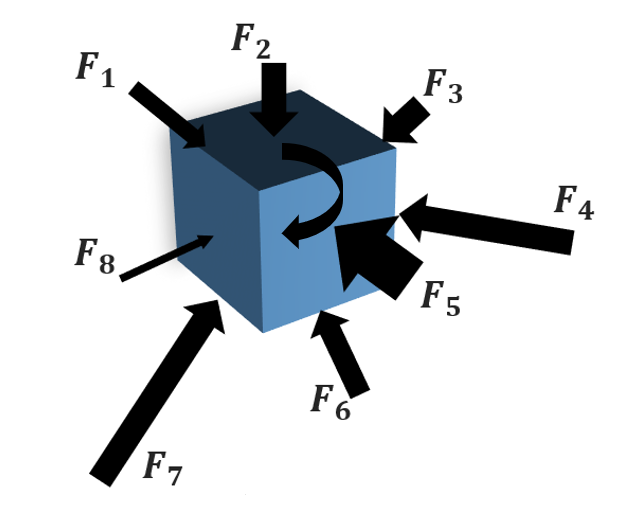
Figura 5 - Definição de Momento Resultante
A explicação mais simples para isso é que obriga-se que os momentos de cada uma dessas forças se anule. Dessa forma, temos na equação 10 o segundo princípio da estática.




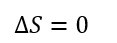
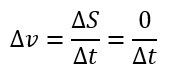
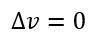
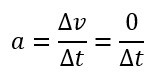
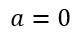
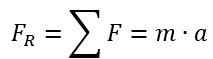
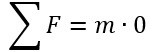
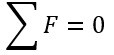
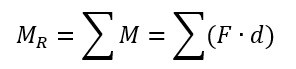
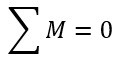










2 comentários para esse post