O que é o Momento de Inércia?

Começarei fazendo-lhes um questionamento:
O que é momento de inércia de um corpo?

“É a resistência à rotação de um corpo”, muitos de vocês devem ter pensando em responder.

Mas, sinto a estranha necessidade de corrigir esta afirmação. Primeiramente por ser uma definição simplória demais para algo já simples. Segundamente por ser um conceito mais físico do que simplesmente verbal. E já que a física utiliza a matemática para se expressar, precisamos entender que a Engenharia se utiliza matematicamente dos fenômenos explicados por químicos e físicos para manipular a natureza dos materiais a fim de que esses assumam formas e funções úteis à sociedade.

Vamos quebrar a resposta que a maioria dos leitores daria para explicar. E para explicar, vou perguntar. A primeira pergunta que quero que seja respondida é:

O que é resistência?

Existem várias respostas possíveis pra esta pergunta. Para um físico, pode ser a necessidade de forçar mecanicamente um material até que ele se rompa e expressá-lo em MPa, por exemplo. Para um químico, pode ser a necessidade de alteração de condições ambientais para uma reação acontecer (temperatura, pressão...). Para um general do exército pode expressar o ato de contrapor um pelotão inimigo até que cheguem reforços ao campo de batalha. Mas, em todos os casos, a idéia central é que resistência significa a tendência à manutenção de um estado atual. Que na primeira pergunta feita (O que é momento de inércia de um corpo?), este mesmo conceito está expresso na palavra “Inércia”.

Outra pergunta: O que é Rotação?

Rotação é um movimento circular. Acho que isso é consenso geral. Mas, para que a rotação ocorra, é necessário que algo gere o movimento. Um carro parado precisa ser acelerado para frente (aceleração tangencial) e ao virar o pneu, geramos um atrito que faz um desvio nessa aceleração para que sempre tangencie o círculo. O atrito dos pneus no asfalto manterá o carro no anel do círculo. Esta aceleração tangencial empurra a massa do carro, isso exprime a existência de uma força (F=ma). Se tomarmos o ponto central desse anel circular de movimento (órbita) deste carro como referência, força vezes o raio da circunferência é o mesmo que momento. Esse conceito está na pergunta feita, também.

Então, quando faço a pergunta “O que é o Momento de Inércia de um corpo?” e vocês me respondem com “É a resistência à rotação de um corpo”, vocês estão me respondendo o óbvio. A palavra inércia exprime o conceito de resistência e a palavra momento exprime a idéia de rotação. É como se o diálogo fosse:

- O que é o Momento de Inércia?

- Momento de Inércia.

Vêem que não faz sentido? Sempre que alguém me responde dessa forma, essa pergunta, eu sei que a pessoa não entendeu o conceito ainda. Portanto, trouxe este texto para explicar o que é o momento de inércia tão utilizado na mecânica das estruturas para equacionar vários outros conceitos, como veremos em outras futuras publicações deste blog.

E para iniciar, não há jeito melhor do que utilizando os conceitos já citados aqui. Vamos falar então de movimento e rotação. Para isso, vamos utilizar uma viga com uma seção em um formato retângular. Imagine que seja uma viga feita com uma tora de madeira ou um material uniforme. Essa viga, na figura 2, tem um centro de gravidade, que é o ponto onde a massa se concentra. De forma simples, a figura 1 explica o conceito de centro de gravidade. Qualquer corpo, preso por um fio em um ponto qualquer tem a tendência de alinha o centro da terra com o ponto onde o fio está preso e o centro de gravidade do corpo. Se fizermos isso várias vezes traçando uma linha vertical, onde essas várias linhas se cruzarem, será nosso centro de gravidade.

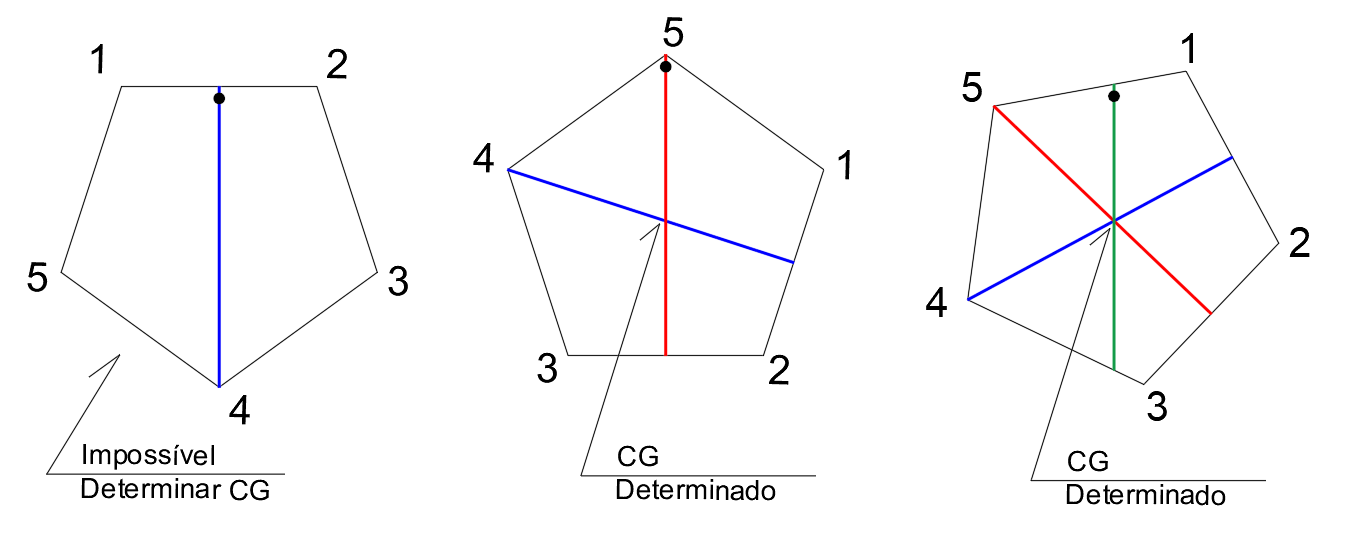
Figura 1 – Método gravitacional para definição do Centro de Gravidade

Figura 2 – Viga exemplo

A partir desta viga, vamos iniciar um movimento de flexão como mostrado na figura 3. Esse movimento ocorre em torno do centro de gravidade. Como a seção da viga é a mesma em todo o seu comprimento, então os centros de gravidade estão alinhados e participam do que chamamos “Linha Neutra”, que é uma linha onde, durante a flexão, não ocorrem deformações horizontais (apenas deslocamento vertical).

Figura 3 – Flexão da viga exemplo

As seções sofrem deformações conforme mostra a figura 4 em vista lateral. A figura 4ª mostra a viga indeformada. A figura 4b, mostra a viga deformada. Selecionamos uma mesma seção dessa viga (tanto deformada quanto indeformada) e essa seção, para os dois casos, foi isolada nas figuras 4c e 4d. A figura 4e mostra a sobreposição dessa seção deformada e indeformada.

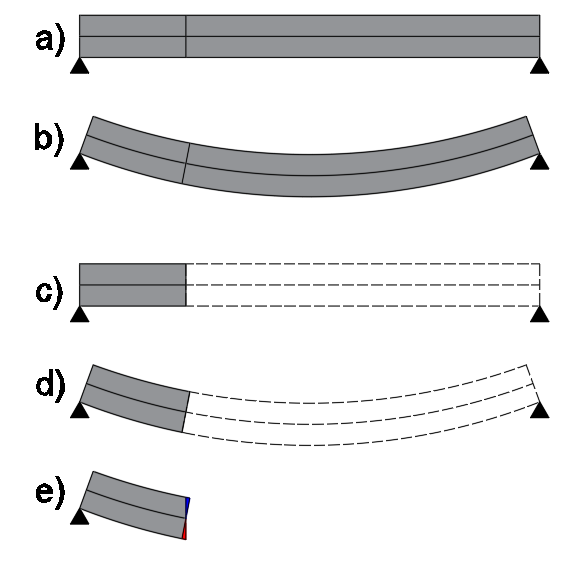
Figura 4 – Deformação da seção

A seção mostrada na figura 5a mostra a figura 4e em vista isométrica. As figuras 5b, 5c e 5d mostram a seção isolada (em suas configurações deformada e indeformada), a seção com um elemento infinitesimal destacado e a seção com seus eixos de análise apresentados, respectivamente.

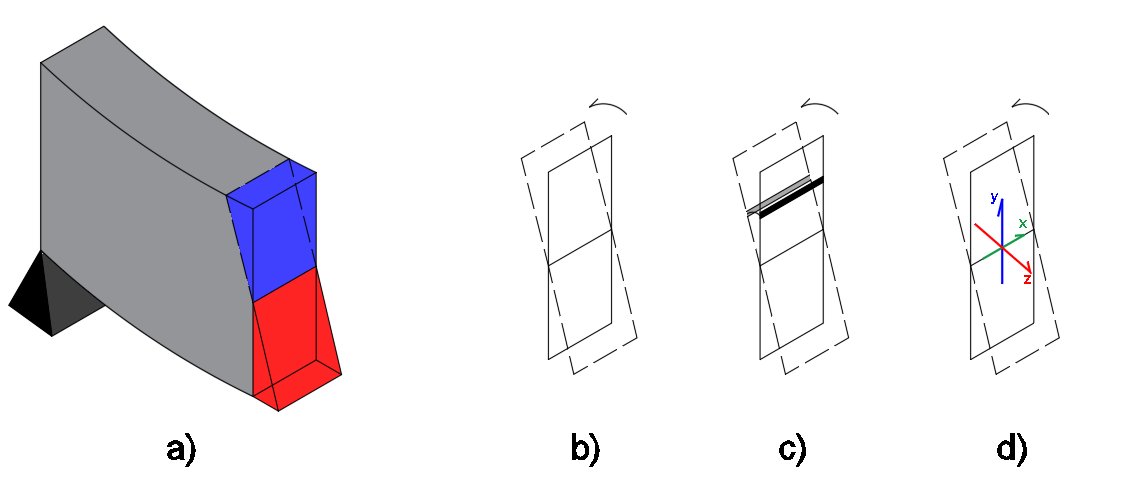
Figura 5 – Seção destacada em isometria

Na seção, vamos isolar um elemento infinitesimal que iniciará um movimento rotacional em torno do eixo neutro da seção. Este elemento será analisado de forma isolada e expandiremos os conceitos e equações paras demais partes da seção da viga. Mas, como todo conhecimento, é necessário aprender as partes e depois estudar o todo. Assim faremos.

Para iniciarmos o entendimento matemático deste movimento, de forma simples e apenas relembrando o que já sabemos da física, vamos lembrar que todo movimento ocorre em função de uma energia cinética necessária para que ele ocorra, expressa pela equação 1. Sendo, o movimento circular, como mostra a figura 6, a velocidade angular é expressa pela equação 2.

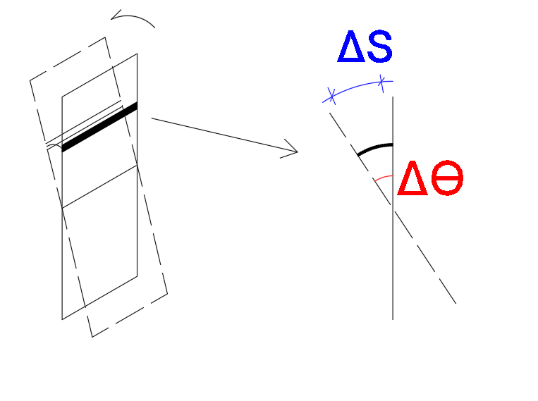
Figura 6 – Esquema do movimento da seção

Considerando que o comprimento de um arco de circunferência é descrito pela equação 3, bastando lembrar que o comprimento total de uma circunferência é 2pr, sendo 2p o ângulo em radianos e r, o raio da circunferência.

A velocidade escalar desse movimento é, então expresso pela equação 4.

E, observando a equação 4, podemos identificar uma relação dela com a Eq. 3. Reescreveremos a Equação 4 e obteremos Equação 5.

Podemos observar que na equação da velocidade linear, existe a equação da velocidade angular. Ou seja, podemos reescrever a Equação 5 como mostra a Equação 6.

Substituindo a velocidade da Equação 1 pela expressa na Equação 6, obtemos a Equação 7.

A partir de então, gostaria de relembrar a equação que expressa a massa específica dos materiais na Equação 8.

Sendo V, o volume; m, a massa e g é a massa específica. Podemos reescrevê-la conforme a Equação 9 e substituir a Equação 9 na Equação 7 obtendo a Equação 10.

Falando, agora, em Geometria, podemos discretizar o volume como sendo a área da base (A) vezes o comprimento do prisma (l)(chamado se altura se o prisma for orientado verticalmente, que não é o nosso caso, pois a viga em estudo é horizontal). Isso é expresso na Equação 11. Vamos substituir essa equação na Equação 10, obtendo a Equação 12.

A partir de então, aplicaremos os conceitos físicos e geométricos vistos nas equações 1 a 12 (sim, não falamos nada de engenharia até agora) para compreender o conceito de Momento de Inércia. Nosso elemento infinitesimal pode ter a forma que desejarmos. Qualquer uma das formas mostradas na figura 7 ou as que você desejar e conseguir descrever (mas que siga alguma lógica). Aconselho a utilização da forma mostrada na figura 6a por um motivo básico: como o elemento infinitesimal possui altura tão pequena que aproxima-se de uma linha (conceito de infinitesimal), então todas as suas partes percorrerão o mesmo percurso (no sentido do movimento de deformação da viga). Assim como as formas infinitesimais da figura 7b e 7c. Mas, para o elemento retangular, o 7a torna-se simplificado por não ter mudança em sua largura no decorrer da forma total da viga. Aproveitamos para fazer uma mudança de variáveis alterando a nomenclatura do raio (r)  para y com a simples finalidade de exprimir que o centro de gravidade do elemento infinitesimal sempre será coincidente com o eixo y da seção (ou, altura da lamela analisada), já que a rotação da seção em flexão dá-se em torno do eixo x definido (veja a figura 5c).

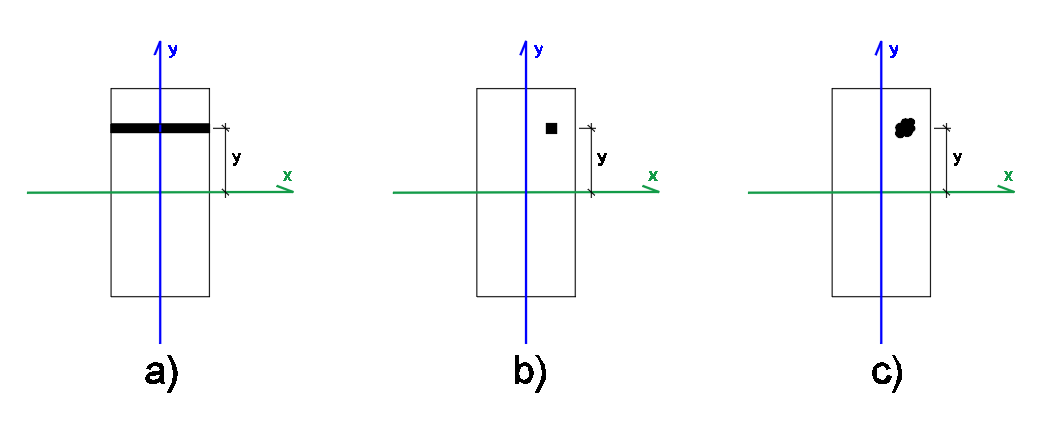
Figura 7 – Algumas das formas possíveis do elemento infinitesimal

Transformando a Equação 12 para relações infinitesimais, obtemos a equação 13. Lembrando que só não se torna infinitesimal aquilo que varia ou no comprimento da viga, ou na posição do elemento infinitesimal ou no material componente. Lembrando que nosso material da viga é homogêneo, então não temos perturbação em seu peso específico (g). Também, não altera-se a velocidade angular (ω), já que o ângulo de rotação da seção da viga é o mesmo. O comprimento da viga não muda (l), não importa qual a dimensão do nosso elemento infinitesimal ou sua posição na seção. O raio (r), mesmo variando pela posição do elemento infinitesimal, não pode ser considerado infinitesimal pois pode ter até mesmo dimensão de metade da altura da viga (a distância entre a LN e a lamela mais tracionada ou mais comprimida). Com isso definimos a Energia Cinética infinitesimal do Elemento Infinitesimal.

Assim, para obtermos a Energia Cinética Total, basta integrarmos a equação 13 em dA. Montando a Equação 14.

Obtida e equação infinitesimal e integrando-a, podemos afirmar que a integral da parcela infinitesimal da energia cinética é a Energia Cinética Total como expressa a equação 15.

Podemos também nos utilizar da propriedade das integrais das constantes. Essas podem sair da integral. Então tudo o que for constante nessa área sairá. Vamos verificar quem depende da “mudança da posição ou dimensão do elemento infinitesimal?”. As únicas parcelas dependentes são o raio e a área do elemento infinitesimal (dA). Assim, montamos a equação 16.

Pois, bem. Em mãos da equação da energia cinética da rotação de toda a seção, apenas a última parcela (a integral) é chamada de Momento de Inércia. Ou seja, o composto da Equação 17 que reescreve (substituindo na equação 16) a equação 18.

Dessa forma, podemos conceituar mais corretamente a Energia Cinética como sendo:

“A parcela proporcional geométrica da energia cinética armazenada na rotação de uma seção”

Explicando melhor esse conceito, uma viga ao sofrer deformações causadas por efeitos de momentos fletores, por sua vez, causados por carregamentos solicitantes, armazena Energia. Essa Energia só é Cinética durante o movimento de deformação. Ao cessar o movimento, essa Energia transforma-se em Energia Potencial de Deformação.

Potencial de quê? Potencial de retorno. Ou seja, em regime linear elástico, a viga tende a voltar à posição inicial (porque seu material está em regime linear elástico, e também tende a voltar a sua deformação inicial nula). Na verdade, a viga volta porque o material volta.

Calculando o Momento de Inércia de uma seção retangular, podemos definir dA como sendo a multiplicação de b e dy, já que todos os elementos infinitesimais do tipo mostrado na figura 6a tem mesma largura b e altura variável. A altura do elemento infinitesimal (dy) varia de -h/2 a h/2. Montamos a equação 19.

Como as variáveis saem da integral, extraímos b e integramos y². assim, obtemos a equação 20 e basta fazer as substituições como mostrado na equação 21 e equação 22 simplificados na equação 23 e 24, resolvido na equação 25 que exprime a famosa “fórmula” do momento de inércia flexional em x para seções retângulares.

Qual é a importância disso?

A partir desse conceito, no futuro, aprenderemos sobre análise de estruturas hiperestática. E o conceito base da hiperestática é o conceito de energia de deformação. Portanto, estamos começando a entrar no fantástico mundo da Análise Estrutura, que é uma parte da Mecânica Das Estruturas. Sejam bem vindos!