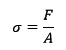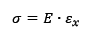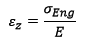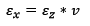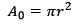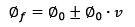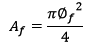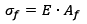Mais uma vez começaremos revisando conceitos básicos utilizando a ciência dos materiais. Mas, prometo que o próximo texto basear-se-á em outa disciplina para não ficar enjoativo. Vamos relembrar pela milésima vez nosso plano de grão? O mesmo está mostrado na figura 1.

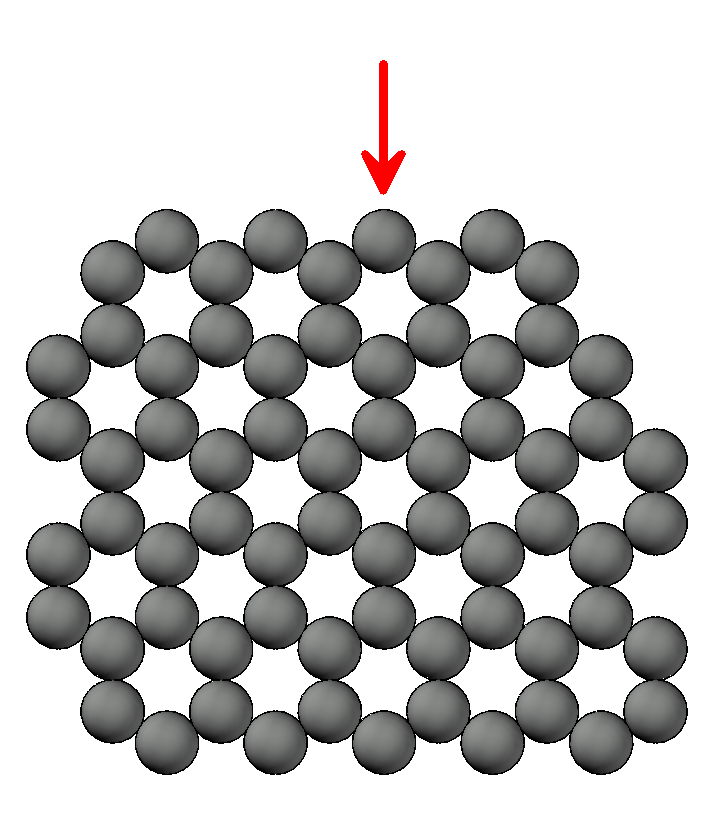
Figura 1 – Plano de Grão

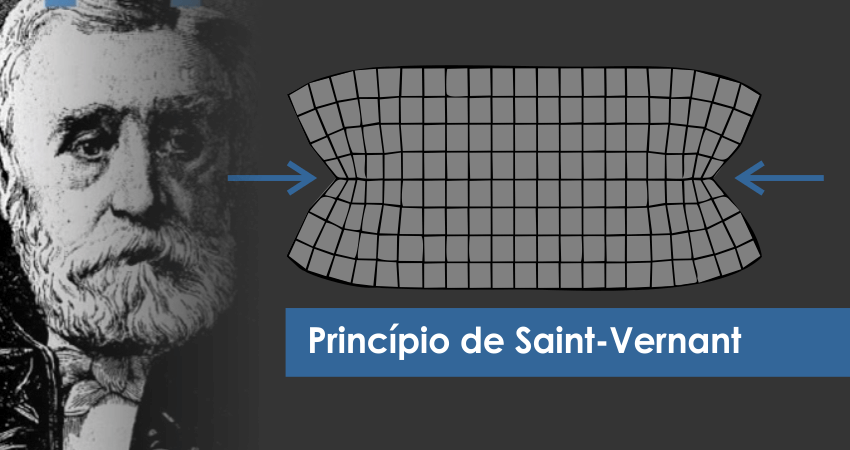
Como foi visto no texto “Coeficiente de Poisson”, os corpos de prova sob carregamento tendem a sofrer alterações em suas dimensões transversais e longitudinais como mostram as figuras 2 e 3.

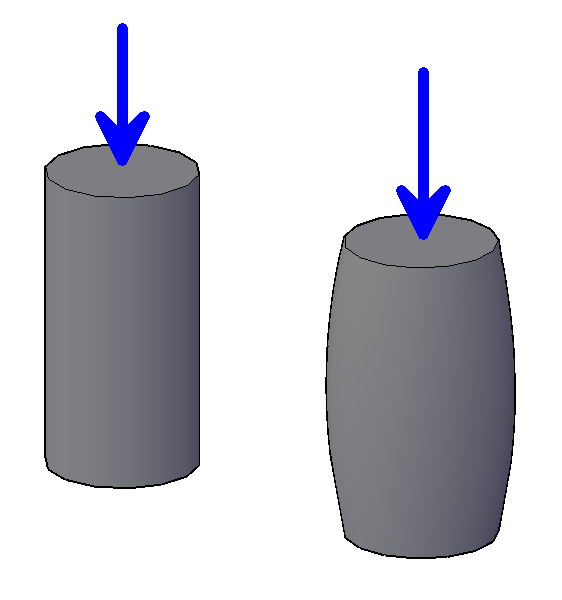
Figura 2 – Mudança nas dimensões de um corpo de prova cilíndrico devido à compressão

Figura 3 – Mudança nas dimensões de um corpo de prova cilíndrico devido à tração

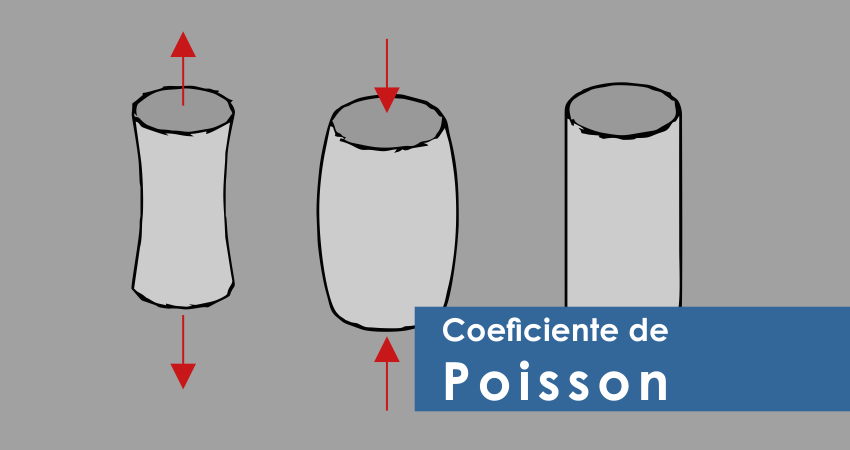
Isso gerou o que descrevemos como Efeito de Poisson matematizado no Coeficiente de Poisson. Ainda, retornando nos conceitos, recordemos as equações de tensão mostradas nas equações 1 e 2. Repare que a tensão tanto sofre efeito da alteração dos valores de área (conforme equação 1) quanto dos valores de deformação específica (conforme mostra a equação 2). Não é por acaso. Basta lembrar que as deformações transversais alteram a área transversal. Portanto, é apenas uma consequência.

Para tal, podemos se conhecermos o incremento de carga (passo de carga) de um ensaio, e o coeficiente de Poisson do material ensaiado, calcular a área incremental para cada carga incrementada, avaliando assim, a área nova, recalculando as tensões para cada incremento de carga e incremento de área (podendo, o cientista, inclusive fazer corpos de prova exclusivos para determinação de cada dado desejado: Módulo de elasticidade, Coeficiente de Poisson e Tensão Máxima Resistente à tração e à compressão).

A essa tarefa, você verificará que, se, na equação 1, você elaborar um gráfico do incremento de carga (F) sem considerar o aumento da área devido ao Efeito de Poisson, obterá uma tabela de valores de tensão (σ). E se fizer o mesmo recalculando o valor da área a cada incremento de carga, obterá outra tabela de valores de tensão. À tensão que não considera o Efeito de Poisson, damos o nome de Tensão de Engenharia. A tensão que considera esse efeito, denominamos Tensão Real.

Como forma de exemplificar, foi elaborada a tabela 1 que considerou um corpo de prova cilíndrico sub tração e sob compressão. Foram utilizadas as equações 3 a 8 para montar a tabela. O corpo de prova utilizado tinha diâmetro de 10cm e altura de 20cm. Concreto de 40 MPa de resistência axial considerando-o totalmente linear elástico. Módulo de Elasticidade de 35.417,5 MPa e coeficiente de Poisson 0,2. Na tabela utilizou-se o passo de tensão de 1 MPa. O gráfico da figura 4 mostra com exagero de 1000x a diferença entre as tensões reais de tração e compressão e a tensão de Engenharia. Lembranco que Af-comp e Af-trac podem ser obtidas através da determinação dos novos diâmetros

Tabela 1 – Cálculo das Tensões Reais de Compressão e Tração

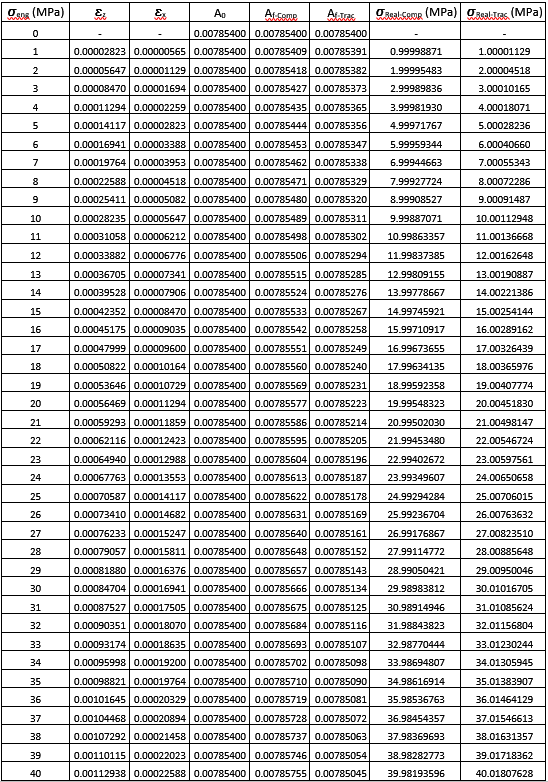
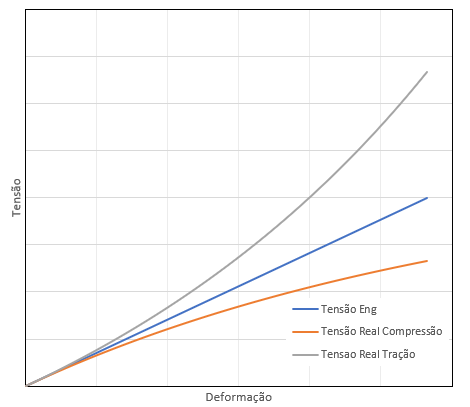
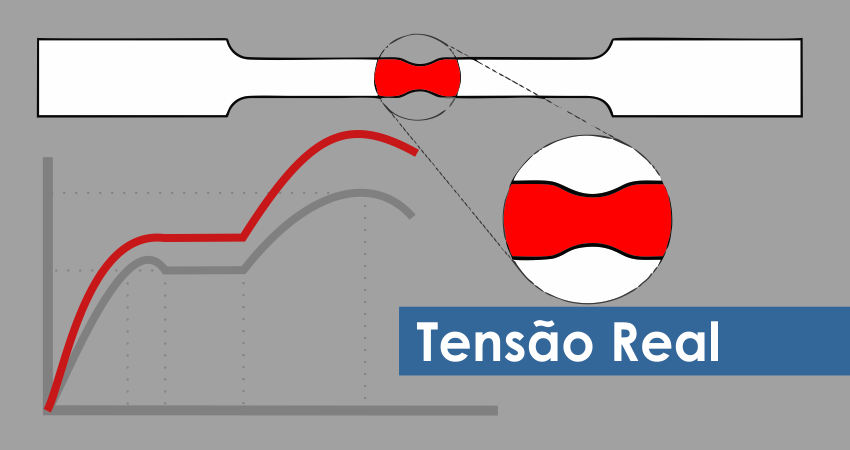
Figura 4 – Comparação exagerada das tensões reais de tração e compressão com a tensão de Engenharia

Repare que a tensão de Engenharia é linear (pra o caso linear elástico do exemplo aqui citado), mas, mesmo no regime elástico as tensões reais não são lineares. Isso se deve a equação das tensões reais considerar a nova área. Ou seja, o incremento de área possui um fator ao quadrado tornando parabólica, a curva das tensões (repare que o incremento de área é aplicado ao diâmetro, que é elevado ao quadrado). Portanto, tornaria-se demasiado complexo utilizar essa equação. O gráfico sem o exagero de 1000x das diferenças entre as tensões reais e tensões de engenharia é apresentado na figura 5.

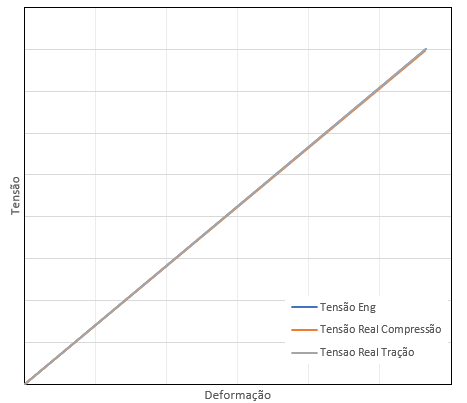
Figura 5 – Comparação não-exagerada entre as tensões reais e de engenharia

Observe que essa diferença, para o caso de um regime elástico é irrisório e pode ser desconsiderado. Portanto, é plausível que utilizemos as teorias simplificadas, pois o trabalho para utilizar todas as equações baseadas em integrais (pois estamos tratando de curvas) é exageradamente trabalhoso quando comparado ao ganho de precisão inferido aos cálculos. Além de termos imperfeições, outras, nos materiais e equipamentos laboratoriais, falta de controles tão precisos que justifiquem ou garantam tal assertividade, entre outros erros tão maiores do que essa pequena diferença mostrada na figura 5.

Observe na figura 4 que as diferenças das tensões sob tração são maiores que sob compressão. Isso se dá devido à compressão amortizar essa diferença devido ao aumento da área de distribuição das forças enquanto a tração reduz essa área aumentando cada vez mais as tensões. Devido a isso, caso existam defeitos nos materiais, ocorrerá mais rapidamente a concentração as tensões ao redor desses defeitos. Como foi mostrado no texto “Por quê ocorre a Flambagem” deste mesmo blog. A figura 6 mostra um efeito extremo de concentração de tensões. Esse efeito é observado como uma redução drástica da seção de uma peça tracionada e é chamado de estricção.

Figura 6 – Corpo de prova estrictado com ampliação

Esse fenômeno ocorre porque, no gráfico tensão x deformação o corpo de prova ultrapassou os limites elásticos (material não alterado), escoou (mudança de posições atômicas na rede cristalina ocupando vacâncias ou contornando átomos intersticiais) e iniciou o processo de  encruamento (ganho de resistência devido ao preenchimento da grande maioria dos defeitos de vacância, onde não é mais possível deformar sem simplesmente aumentar as distâncias interatômicas) e finalmente começou o processo de ruptura por quebra das ligações interatômicas. Esse processo é mostrado na figura 7.

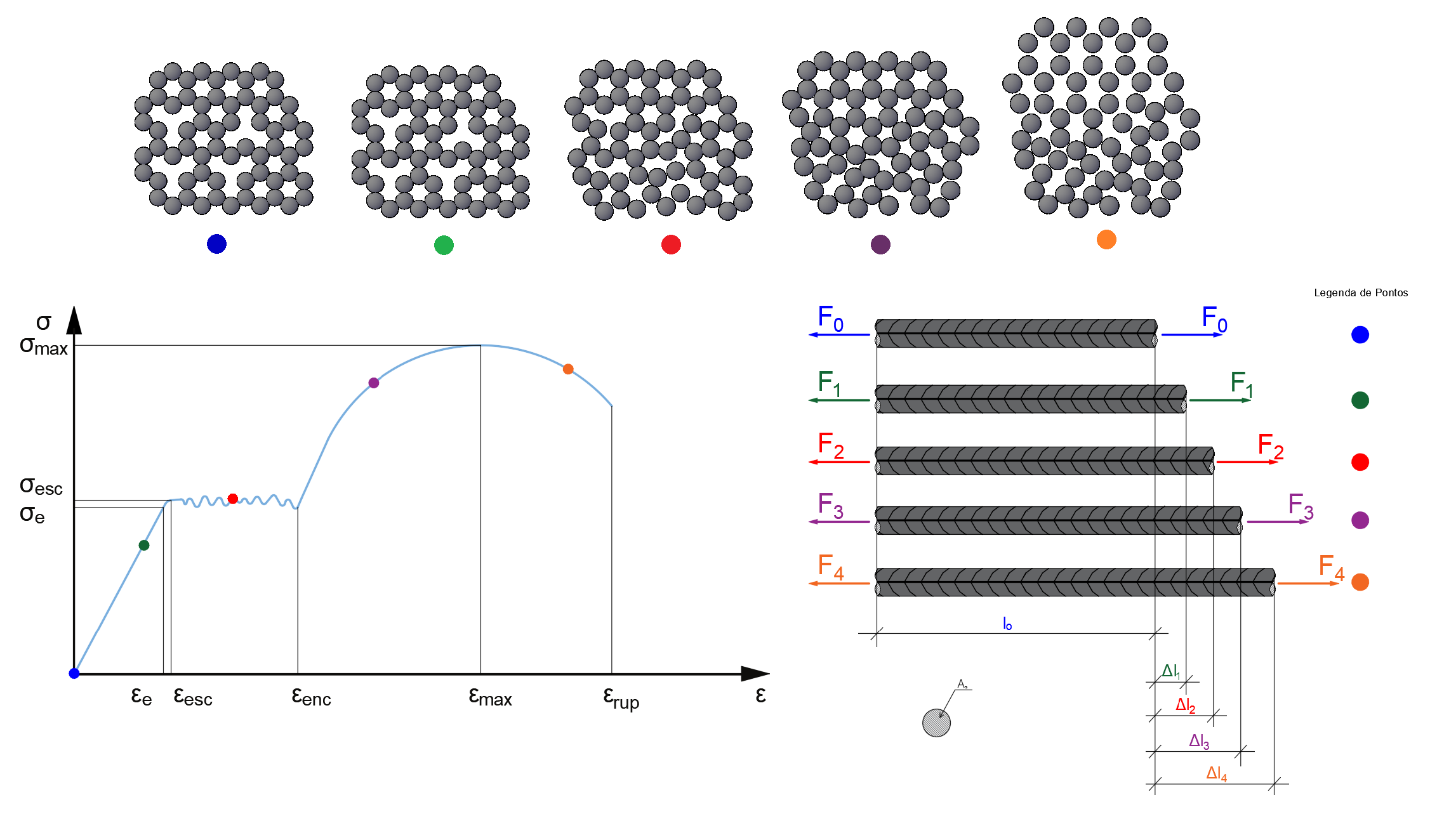
Figura 7 – evolução da alteração do material sob aumento das cargas até seu colapso

A partir do ponto laranja, observado na figura 7, observa-se que, para preencher vacâncias e aumentar seu comprimento, o grão precisou retirar material de suas laterais criando uma seção com menor área (compare a dimensão horizontal da base do grão referente ao ponto azul com a base do grão referente ao ponto laranja). A partir dessa redução de área, ocorre o fenômeno de concentração das tensões na menor área (consequentemente, maiores tensões) que causam a estricção. No entanto, o que se observa no diagrama de engenharia, é uma queda de tensões. Como isso seria possível?

Simples! O diagrama tensão x deformação de Engenharia não exprime tensões atuantes, mas, tensões resistentes. Ou seja, a área reduz, portanto possui menor capacidade de suporte de tensão. Então o diagrama sobre uma redução. Caso desejássemos um diagrama de tensões reais, o mesmo teria a configuração mostrada na figura 8. No entanto, não serve para projetos de Engenharia, uma vez que os materiais devem resistir às solicitações. Então não há aplicação prática para este diagrama.

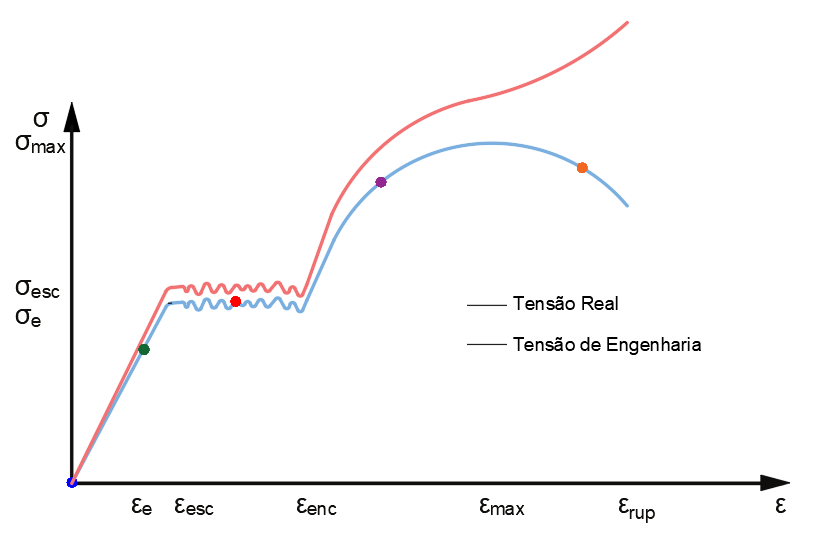
Figura 8 – Diagramas Tensão de Engenharia e Tensão Real comparados

O conhecimento sobre tensões reais apenas é necessário para compreender o diagrama de tensões de engenharia e seu fundamento básico. Afinal, até este texto não havia ficado claro que a tensão medida e impressa no diagrama tensão x deformação era uma tensão resistente, já que sempre eram colocadas forças. No texto “Diagrama tensão x deformação” citamos que a maioria das prensas é controlada por deslocamento. Isso é importante ser salientado, pois as normas indicam equações de tensão em função da deformação. Assim, a prensa fica registrando a deformação causada e a força medida para aquela deformação. Não o contrário. Portanto, de hoje em diante, tenham conhecimento de que tudo o que tratarmos sobre tensões, ensaios laboratoriais, equações e qualquer outro referente ao diagrama apenas exprime aquilo que a prensa entrega ao deformar um material. Então o que temos em mãos é a resposta do material a um estímulo externo chamado deformação.