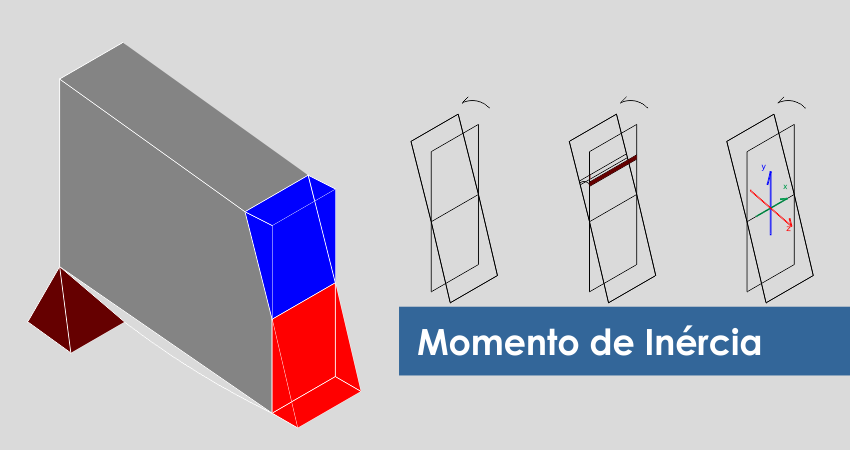
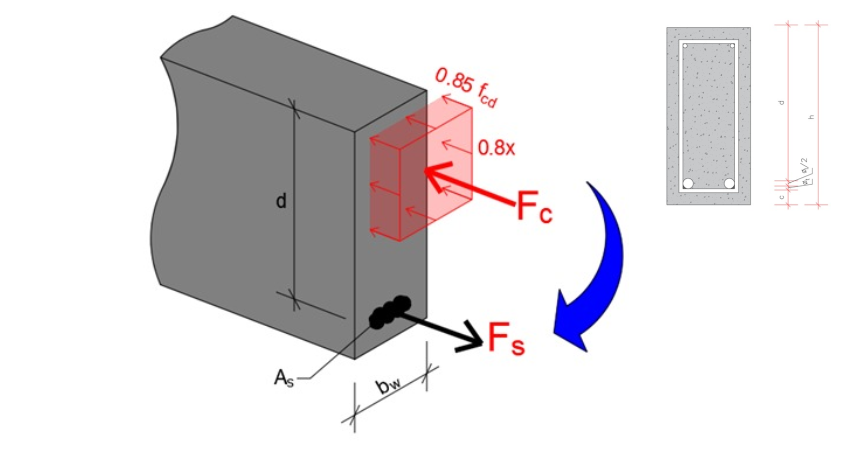
Como foi mostrado no texto anterior “Momento de Inércia”, conhecemos a equação do Momento de inércia e seu método de dedução. Partindo disso, mais precisamente do que é mostrado na figura 1, mas, dessa vez, partindo de uma vista lateral como mostrado na figura 2, vamos compreender como as deformações geram tensões axiais.

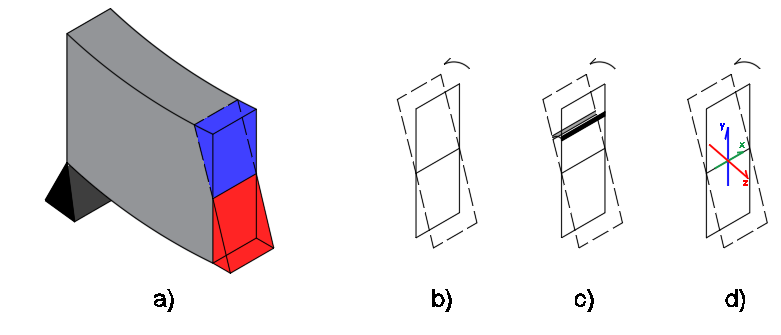
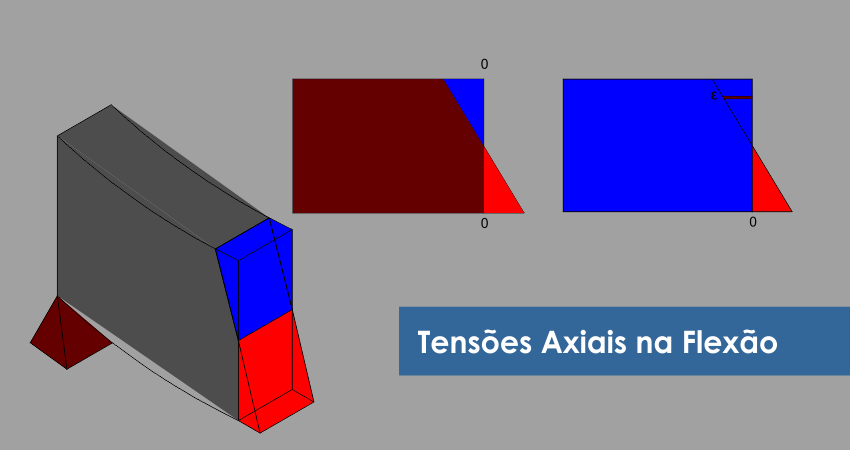
Figura 1 – Deformações na seção da viga

As deformações no elemento infinitesimal mostrado na figura 1c é mostrada na figura 2c. A fim de prever o valor desta deformação, fazemos uma semelhança de triângulo considerando apenas o triângulo azul. Esse procedimento geométrico, no entanto, apenas é possível quando conhecemos as deformações na viga, que não é o caso em estruturas usuais por não dispormos, normalmente de instrumentação de monitoramento das estruturas. Assim, confiamos, para atividades de projetos de reforço e análises de patologias, nas cargas previsíveis (fazemos levantamento das cargas sobre essa viga). Mas, obtendo essa relação, teremos as equações 1 e, simplificando, a equação 2.

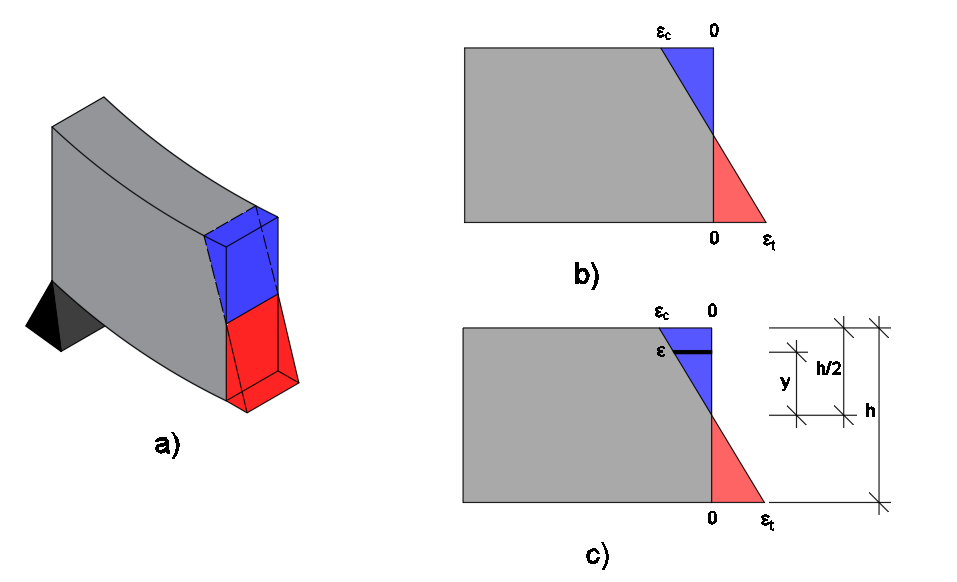
Figura 2 - Deformações nomeadas e cotadas

A pergunta, então é: como, a partir do momento fletor (que ainda aprenderemos a equacionar), podemos prever as deformações nessa viga? Conhecemos a relação de tensão mostrada na equação 3 e o conceito aplicado ao elemento infinitesimal na equação 4.

Organizando para obtermos a força infinitesimal, obtemos a equação 5.

A equação básica de momento é mostrada na equação 6. Seu conceito infinitesimal é mostrado na equação 7, lembrando que a distância de rotação equivale a y.

Sabendo que a tensão máxima de compressão (smáx) causa a deformação máxima de compressão (ec), então, podemos definir as relações mostradas na equação 8 e 9 advindas da lei de Hooke para materiais lineares elásticos sendo, a Equação 6, a lei de Hooke (que também vale para o elemento infinitesimal), a Equação 7, sua aplicação para a tensão máxima.

Isolaremos os módulos de elasticidade das equações 8 e 9 e obteremos as equações 10 e 11, respectivamente.

De posse dos módulos de elasticidade, podemos igualá-los, pois o material é homogêneo, portanto, tem o mesmo módulo de elasticidade em todas as suas partes. Assim, chegamos à equação 12.

Isolando a tensão no elemento infinitesimal, temos a equação 13.

Integrando a equação 7, chegamos à equação 14.

Substituindo a equação 5 na equação 7, chegamos à equação 15.

substituindo a equação 13 na equação 15, chegamos à equação 16.

Agora, substituindo a equação 2 na equação 16, obtemos a equação 17.

Simplificando, obtemos a equação 18.

Reorganizando tirando as constantes da integral, obtemos a equação 19.

Repare se o segundo termo da multiplicação não coincide com a equação da inércia mostrada no texto anterior “Momento de Inércia” e mostrado aqui na equação 20.

Substituindo a equação 20 na equação 19, chegamos à equação 21.

Substituindo a equação 2 na equação 13, temos a equação 22.

Organizando de forma a isolar a tensão máxima, chegamos à equação 23 que, simplificada, chegamos à equação 24 e posteriormente à .

Substituindo a equação 24 na equação 21, temos a equação 25 que, simplificada, obtemos a equação 26.

Isolando a tensão, chegamos finalmente à equação 27.

A equação 27 é a equação das tensões axiais em qualquer lamela da seção de uma viga. Convencionou-se indicar as tensões sempre com seus vetores apontando para a seção indeformada. A figura 3a mostra os deslocamentos da seção da viga em 2D e 3D, e a Figura 3b mostra as tensões da seção em 2D e 3D.

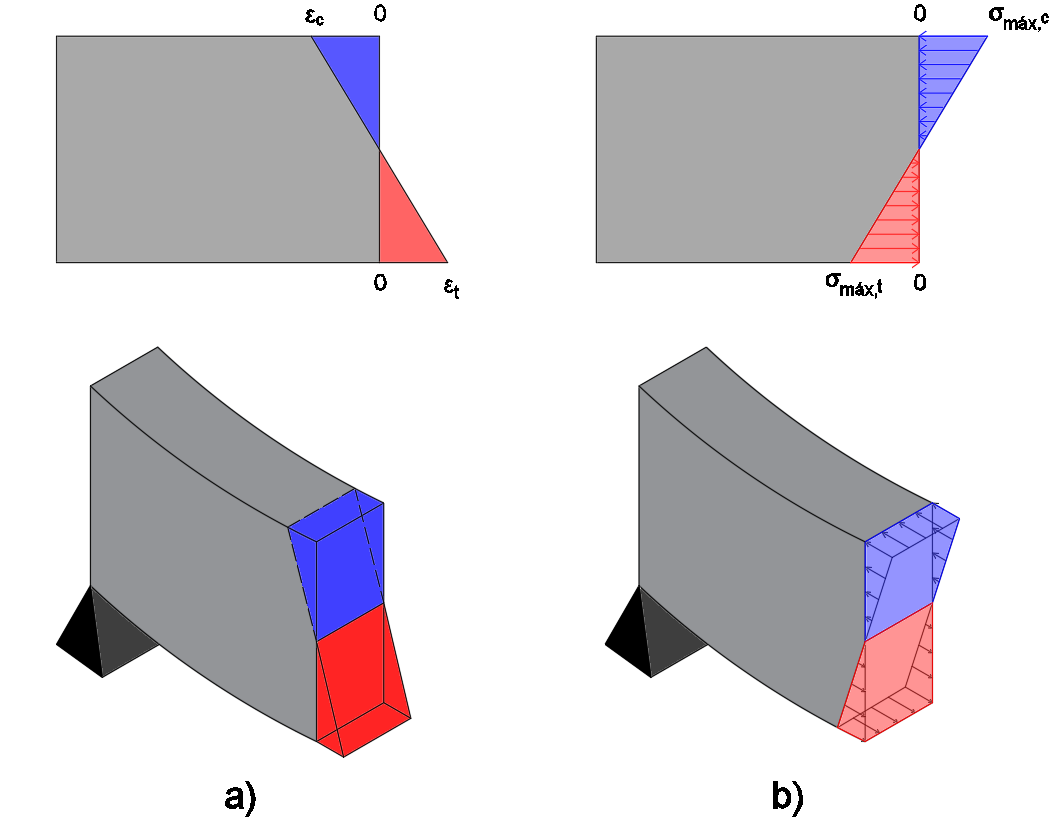
Figura 3 – Deformações e tensões na seção de uma viga

Reparem que o momento de inércia, aprendido no texto anterior intitulado “Momento de Inércia”, aparece na equação das tensões como sendo inversamente proporcional a esta. Ou seja, quanto maior o momento de inércia, menor será a tensão causada por um mesmo momento fletor. Mas, lembrando do conceito de momento de inércia como sendo “A parcela proporcional geométrica da energia cinética armazenada na rotação de uma seção”, e como a dedução da equação de Tensões passa pelas deformações sofridas pelas lamelas dessa tensão, podemos afirmar que o aumento do valor de momento de inércia sendo inversamente proporcional à tensão sofrida, então, a Energia cinética também é inversamente proporcional. Ou seja, menores tensões armazenam menos Energia na viga. Se essa energia é cinética, então menores tensões também movimentam menos a viga. Menores flechas e menores deformações. Logo, podemos afirmar também que A Energia Cinética Armazenada é Diretamente proporcional ás deformações da seção e à flecha sofrida. Essa dedução é o tema do nosso próximo texto.

Repararam como uma coisa puxa a outra!?