Meu sonho desde que ingressei no ensino médio, em 2005, é colocar meu nome no S.I. como uma unidade de medida de alguma grandeza física mesmo que seja relacionando outras duas já existentes como Pascal fez em 1663 postulando a equação da tensão (pressão mecânica) como sendo a distribuição de uma unidade de força (Newton - N) em uma unidade de área (metro quadrado – m²) como escrito na equação 1. Brincadeiras à parte, essa é a grandeza física que inicia nosso texto de hoje.

Eq. 1.

É importante frisar que essa distribuição de cargas em uma área é uma necessidade física. Não existe ponto real. Toda e qualquer aplicação de cargas é aplicada em uma área mínima já que por menor que seja essa superfície, mesmo que em dimensões atômicas, é uma superfície. Os carregamentos passíveis de distribuição são apresentados na figura 1.

Figura 1 - Carregamentos distribuídos uniformemente, triangularmente e genérico, respectivamente

Essa distribuição, no entanto, pode ocorrer em uma área menor do que a totalidade da superfície de um corpo. Quando essas dimensões são convenientemente pequenas, consideramos que esse carregamento seja aplicado em um ponto. Esse ponto, por conveniência e significado físico, é o próprio centro de gravidade da carga distribuída real. Veja a simplificação da carga apresentada na figura 2.

Figura 2 - Conversão de carregamento distribuído em concentrado

A tensão mecânica tende a deformar os materiais onde as cargas atuam. Não por coincidência, o mesmo acontece com as molas quando submetidas a um carregamento qualquer. Para solos, não por coincidência, mas, por falta de criatividade e principalmente por alusão, o termo dado à constante de proporcionalidade de tensões e deformações chama-se “Coeficiente de Mola”.

A equação 2 apresenta a formulação, aprendida no ensino médio e reforçada na disciplina de Física 1 da graduação, para a força de reação de uma mola ao ser deformada. Lembrando que a posição zero é a posição inicial da aplicação de carga e o sinal é escolhido baseado n.

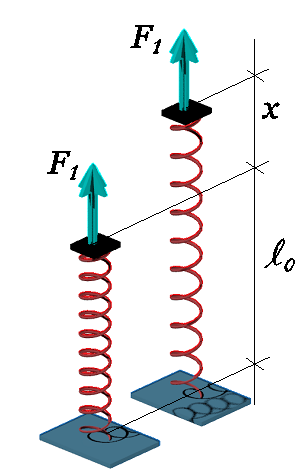
Figura 3 - Mola básica

Essa formulação é muito semelhante à equação 2 apresentada. Com a alteração de que o termo constante (b) presente na equação 2, também chamado de coeficiente linear, na equação 1 possui o valor zero. a=k (coeficiente angular) e f(x)=F que também está em função da posição. A equação 3 é chamada de equação de primeiro grau.

Outra equação nasce do mesmo princípio apresentado na equação 1, a qual denominaremos a partir de agora como sendo a Lei de Hooke (postulada por Robert Hooke em 1676). Essa nova equação correlaciona a tensão com a deformação adimensional (calma, não se desespere. Vamos explicar isso).

Primeiro vamos fazer uma simples alteração na Lei de Hooke (equação 2, lembram!?). mudaremos a variável (x) para o que chamaremos de alongamento/encurtamento (Δl1). Isso monta a equação 4 e é mostrado geometricamente na Figura 4.

Eq. 4.

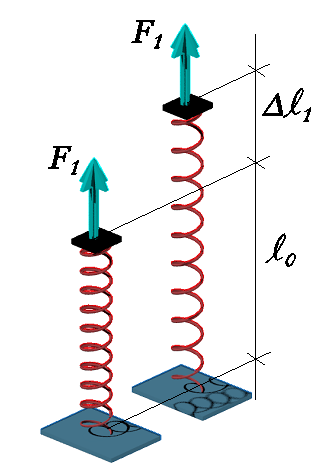
Figura 4 - Mola básica com conversão da nomenclatura do deslocamento

Imaginando que tenhamos duas molas iguais com Coeficiente de Mola (k) iguais associadas em paralelo e aplicamos a mesma força (F1) conforme mostra a figura 5.

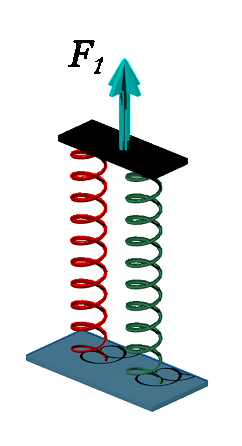
Figura 5 - Molas Associadas em paralelo

Podemos afirmar que esse sistema de molas associado, desde que ambas as molas sejam completamente iguais, serão divididas conforme a figura 6 onde F1 = 2×F2.

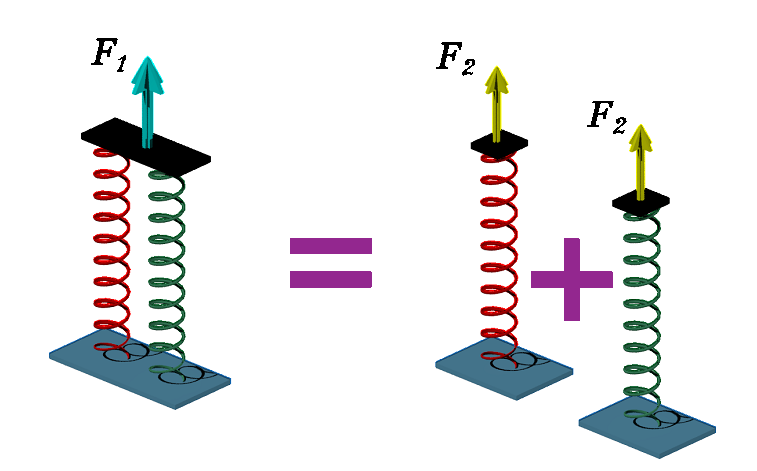
Figura 6 - Discretização do sistema de molas associadas em paralelo em molas básicas com divisão da carga

Com isso, temos que ambos os sistemas divididos sofrem o mesmo deslocamento (Δl2) como mostra a figura 7.

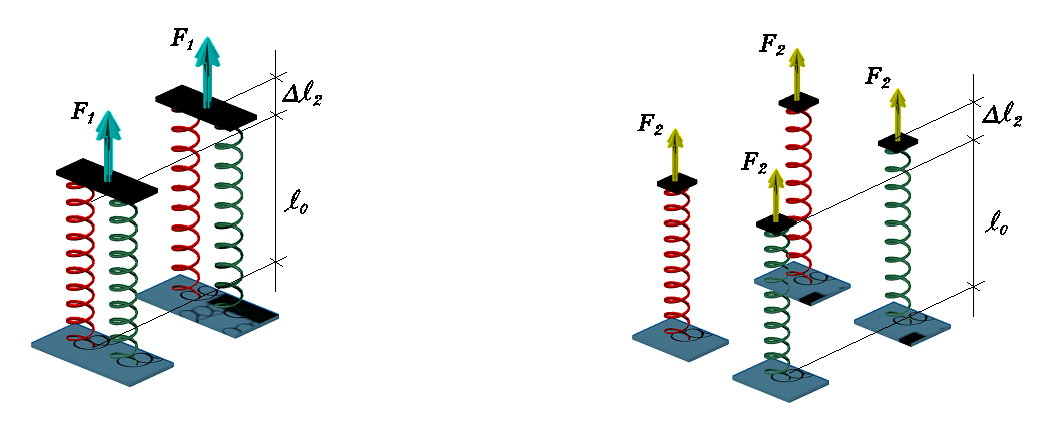
Figura 7 - Comparação entre deslocamentos das molas associadas em paralelo e das molas discretizadas

Para tal, a equação 5 apresenta a solução do sistema mostrado na figura 7 quando comparado com o sistema apresentado na figura 4 regido pela equação 4.

Substituindo a equação 4 na equação 5 e fazendo os devidos tratamentos matemáticos, teremos as equações 6 e 7:

Lembrando da equação 4 e substituindo na equação 7, temos a relação entre os deslocamentos Δl1 e Δl2:

Agora, imaginemos uma nova igualdade onde substituiremos as duas molas mostradas na figura 5 por uma mola equivalente que tenha um coeficiente de mola diferente (k2) do coeficiente das duas molas separadas (k1) como mostra a figura 8.

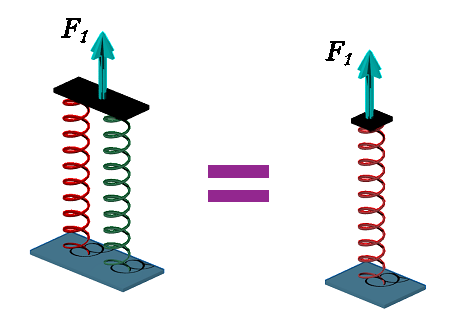
Figura 8 - Conversão do sistema de molas associadas em paralelo em uma mola equivalente

Lembrando que o deslocamento da mola dupla é igual ao deslocamento das molas divididas (Δl2). A equação 10 rege o sistema.

Eq. 10.

Substituindo a equação 4 na equação 10, teremos:

Tomando a equação 9 em substituição na equação 11 e dando os devidos trabalhos matemáticos básicos, obteremos:

Ou seja, a mola equivalente possui mais rigidez que a mola básica. Pode-se afirmar que foi dobrada a área de contato das molas com a placa de carga. Então, o deslocamento reduz pela metade quando dobramos a área, ou seja, são inversamente proporcionais. Isso nos conduz ao conceito de tensão já apresentado. Mas, levaremos isso para um segundo momento.

Fazendo outra analogia, agora associaremos em série, as mesmas duas molas com coeficiente de mola iguais (k1) submetida ao mesmo carregamento F1 como mostra a figura 9.

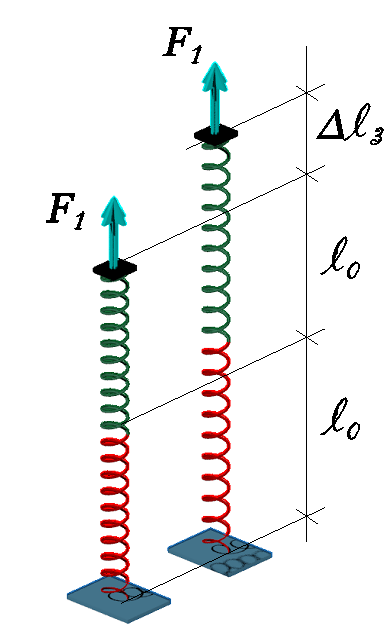
Figura 9 - Sistemas de molas associadas em série

Haja visto que o comprimento inicial das molas indeformadas associadas em série (l02) é a soma dos dois comprimentos iniciais das molas básicas (l0), colocamos a equação 14.

Eq. 14.

Como o mecanismo de deformação dá-se pela transmissão de carga de uma mola para a outra, sabemos que cada uma das duas molas sofrerá a mesma deformação por estarem sujeitas à mesma força. De forma que a deformação Δl3 será a soma das duas deformações Δl1 de cada mola. Essa relação é expressa pela equação 15.

Eq. 15.

Como a mola associada em série é regida pela lei de Hooke, faremos a mesma analogia anterior da mola equivalente conforme mostra a figura 10 e expressa pela equação 16 fazendo com que o seu comprimento inicial seja duplicado, como é o comprimento das molas associadas em série. E criaremos um coeficiente de mola (k3). A equação 17 apresenta esse comportamento.

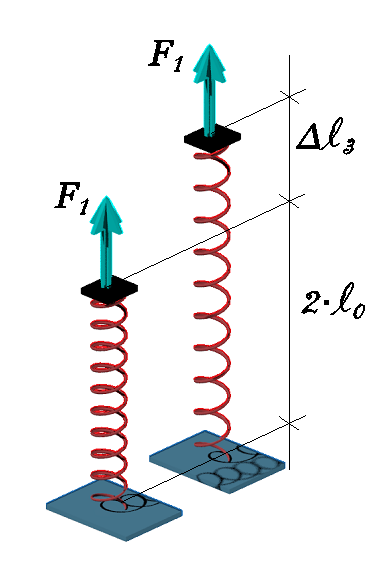
Figura 10 - Mola equivalente da mola associada em série

		Eq. 16.
		Eq. 17.

Substituindo a equação 4 na equação 17, temos equação 18.

Eq. 18.

Operando matematicamente ficamos com a equação 19.

Eq. 19.

Ou seja, a mola equivalente possui menos rigidez que a mola básica. Pode-se afirmar que foi dobrado o comprimento inicial. Então, o deslocamento dobra quando dobramos o comprimento inicial, ou seja, são diretamente proporcionais.

Mas, veja bem. No âmago do problema, as molas equivalentes não existem, realmente. Mas, sim, mudança de área e mudança de comprimento. De forma que comprovamos que para as mesmas molas, o coeficiente da mola equivalente é simultaneamente diretamente proporcional à área e inversamente proporcional ao comprimento inicial. Assim, escreveremos a equação da força resistente equivalente da mola como na equação 20

Eq. 20.

Haja visto que a força equivalente basicamente é a equação da força apresentada na equação 4 com as operações apresentadas no último parágrafo, reescreveremos como na equação 21.

Eq. 21.

Igualando as equações 20 e 21, alterando a posição dos termos teremos iniciais para que tenhamos um coeficiente de mola independente da área e do comprimento inicial caminhamos para a equação 22.

Eq. 22.

O termo de comprimento inicial no primeiro termo será passado para o segundo termo da equação e obtemos a equação 23.

Eq. 23.

Essa mudança nos dá uma relação simples que melhor organiza as relações anteriores fazendo com que os deslocamentos sejam “percentualmente” relativos ao seu comprimento inicial. Veja: Agora, como ao dobrar a carga dobrávamos o deslocamento, esse novo termo (Δl/l0) não sofre alteração. Da mesma forma, quando dividíamos a força quando dobrávamos a área, tendo, assim, metade da força para cada mola associada em paralelo, e obtínhamos metade do deslocamento, esse termo também não sofre mais alterações. Ou seja, ele se torna independente da área e somente dependerá da relação de mudança do comprimento inicial, para uma mesma força.

A primeira parte da equação sugere o primeiro conceito tratado nesse texto: Pressão mecânica ou, também chamado de Tensão. Comparando com a unidade Pascal (Pa) mostrada no início do texto, temos a equação 24.

Eq. 24.

Tal que foi nomeado, o primeiro termo da multiplicação, de Módulo de Elasticidade/Young (E)¹ e o segundo por deformação específica (ε), temos a equação proposta por Leonard Euler, comprovada pro Riccati. Young foi somente homenageado (Truesdell, 1960). Ficamos com a equação 25.

Eq. 25.

Geometricamente:

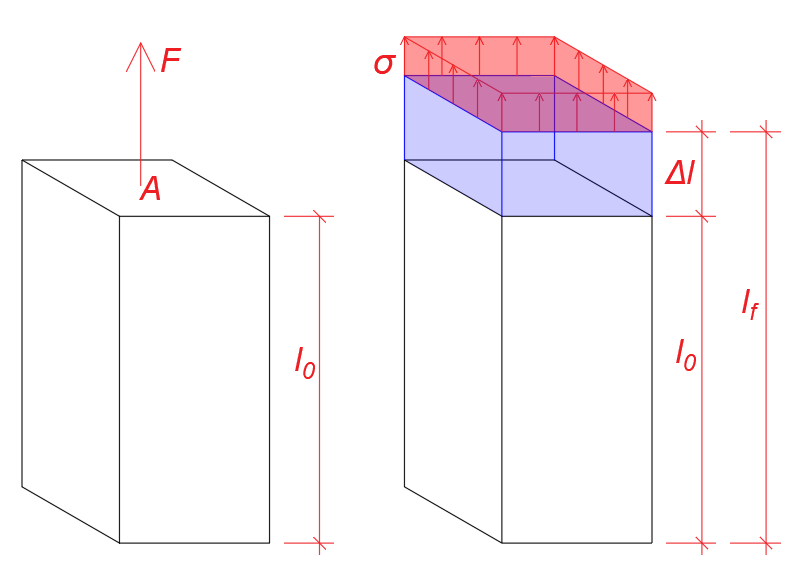
Figura 11 - Significado geométrico da equação que relaciona tensões e deformações

Referências:

Euler, L., Truesdell, C., The Rational Mechanics Of Flexible Or Elastic Bodies. Ed. Springer Science & Business Media. 1960. 421 pág.