Estádios de Tensão

Quando falamos de estádios de tensão, estamos falando de critérios relativos à seção, não à viga como um todo. Portanto, é importante salientar que, dependendo dos esforços atuantes em cada seção de uma viga (consideradas infinitas), teremos infinitos estádios de tensão e infinitos domínios de deformação.

É importante tratar sobre os materiais participantes da seção, uma vez que cada um se comporta de maneira particular e são suas propriedades que modificam o funcionamento das estruturas. Ao mesmo tempo, cada mudança no comportamento das tensões nos materiais e, consequentemente, as deformações das vigas influenciadas pelas tensões, alteram o comportamento da estrutura tanto em seu estado íntegro quanto ao colapso. Por isso precisamos compreender esses dois temas a fim de torná-los realmente aplicáveis à prática da boa Engenharia.

As propriedades dos materiais são, na verdade, seu comportamento-resposta frente à diversos estímulos. A depender do comportamento esperado o desejado, é possível que sejam reforçados a fim de alterar um comportamento considerado inadequado e torna-lo aceitável. As propriedades podem ser relativas a estímulos de carga, deformação, propagação de trincas, propagação do som, temperatura, absorção d’água ou qualquer outro estímulo que se deseje compreender. Sobre as vigas e nosso tema em específico, apenas os estímulos mecânicos de resposta à aplicação de forças serão importantes.

Ainda sobre esses, os estímulos de longa duração são os que tratamos, já que as construções são bens de consumo duráveis com longa vida útil de projeto. Dos materiais estudados, trataremos sobre estruturas de concreto armado, o que nos obriga a conhecer os comportamentos-resposta de dois materiais: O concreto, com bom comportamento às tensões de compressão e frágil à tração, e o aço, seu reforço à tração que visa melhorar o comportamento da peça onde ocorre a falha do concreto e torna adequado o comportamento do elemento.

Relativo ao concreto, é preciosa, a compreensão do seu funcionamento. É um material que não obedece totalmente ao regime elástico, possuindo, comportamento curvilíneo. Para o aço, após a saída do regime elástico, o comportamento volta a ser linear horizontal. A NBR 6118 (ABNT (2014) utiliza os parâmetros mostrados na figura 1 como comportamento padrão do concreto à compressão.

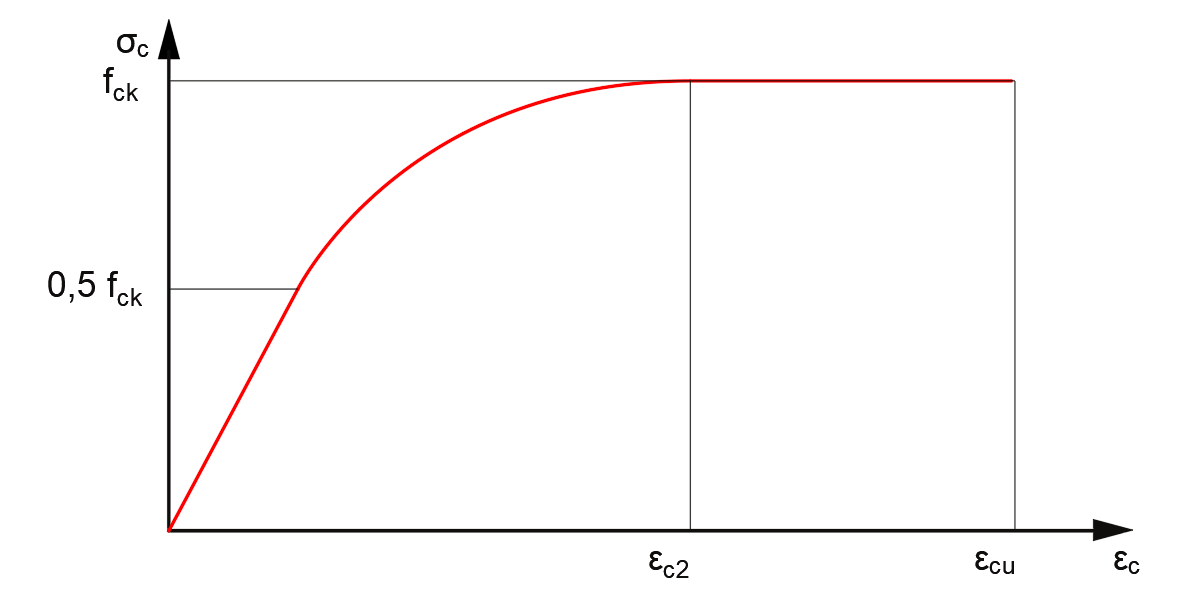
Figura 1 – comportamento do concreto à compressão

É possível observar que a equação é considerada linear até metade da sua resistência característica (0,5 fck), possui uma parcela curva até alcançar a resistência característica (fck) e torna a ter um comportamento linear horizontal apenas deformando-se sob a mesma tensão. Para as armaduras, o comportamento é descrito conforme a figura 2. Observe que para a NBR 61118 (ABNT, 2014) até seu escoamento o aço tem comportamento totalmente linear elástico mantendo comportamento escoado até a ruptura.

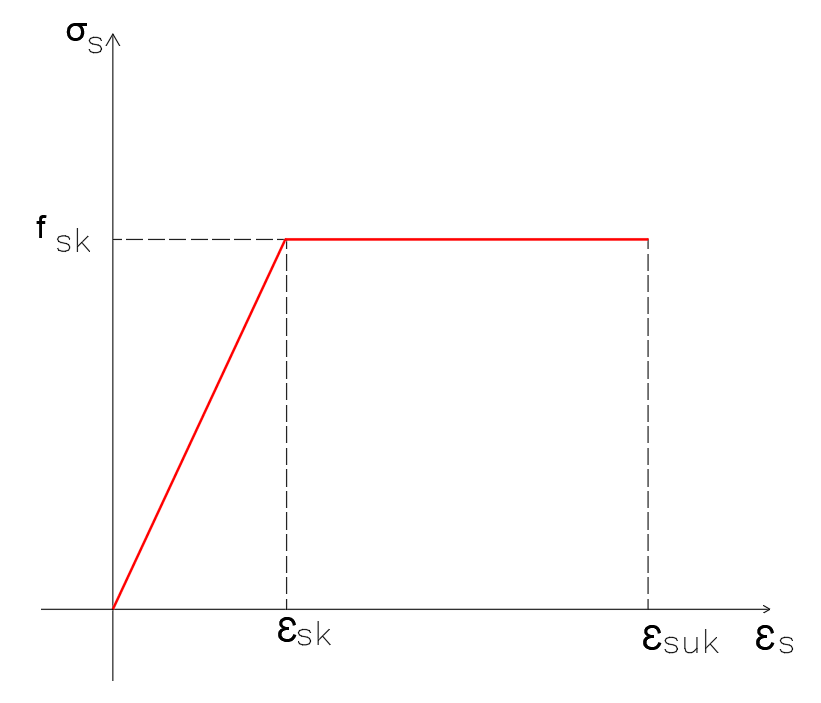
Figura 2 – Comportamento do aço à tração

A falta de confiabilidade em diversas etapas laboratoriais e de obra, no entanto, obrigaram os códigos normativos a utilizarem coeficientes de segurança que garantissem que em nenhuma instância obtivéssemos valores menores do que aqueles calculados. A NBR 6118 (ABNT, 2014) indica a minoração das resistências características (fck e fsk) indicadas nas equações 1 e 2 (Para concretos de até 50 MPa) para resistências de cálculo (fcd e fsd). O fcd é ainda reduzido para 85% de sua resistência devido ao efeito Rush, as resistências minoradas estão indicadas nas equações 3 e 4. Os módulos de elasticidade estão mostrados nas equações 5 e 6 e as resistências de cálculo e características são mostradas comparadas nas figuras 3 e 4.

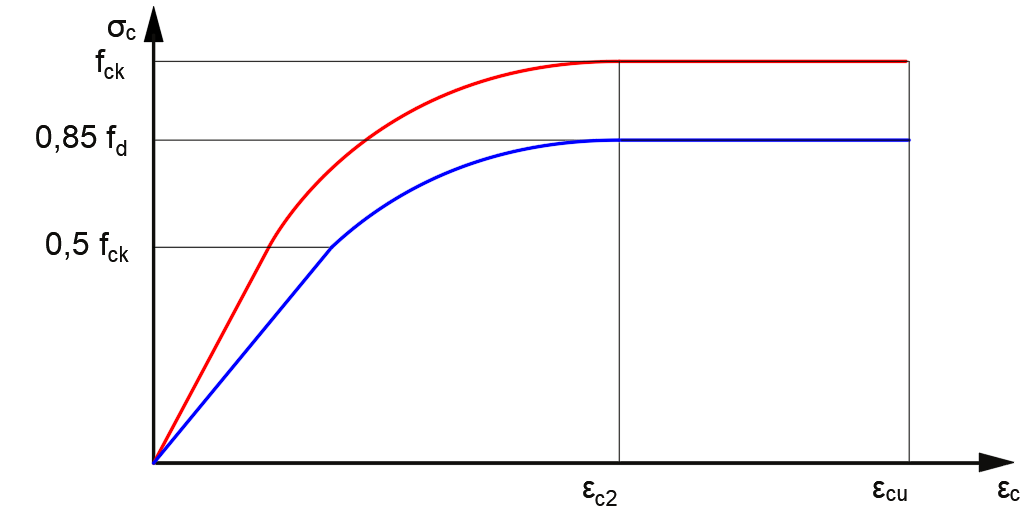
Figura 3 – Comportamento minorado do concreto

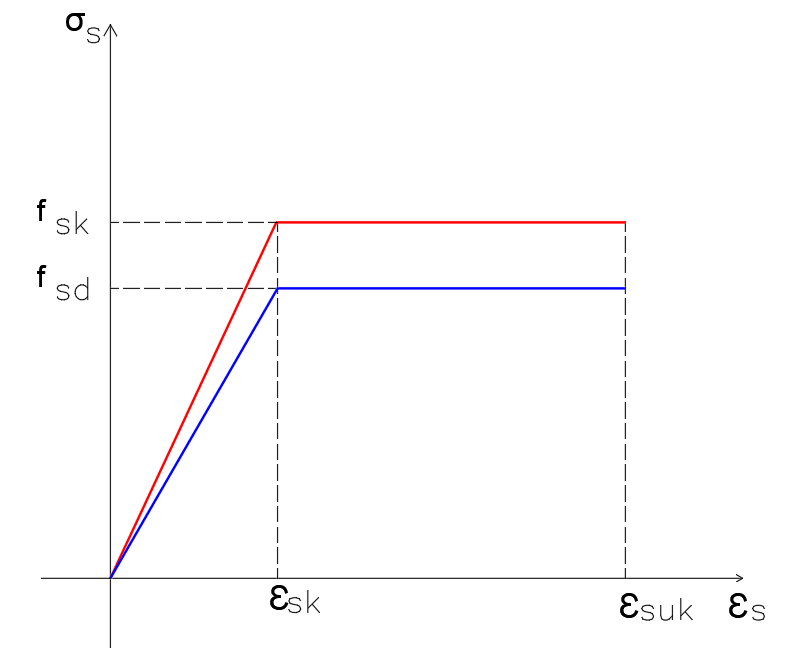
Figura 4 – Comportamento minorado do aço

Os estádios de tensão são caracterizados por mudanças físicas internas da seção de concreto. Como o concreto armado é configurado pela existência do aço embebido em concreto como forma de reforçar a estrutura pós fissuração, então, a primeira alteração física é caracterizada pela fissuração do concreto. A equação 7 presenta o valor da tensão de fissuração do concreto.

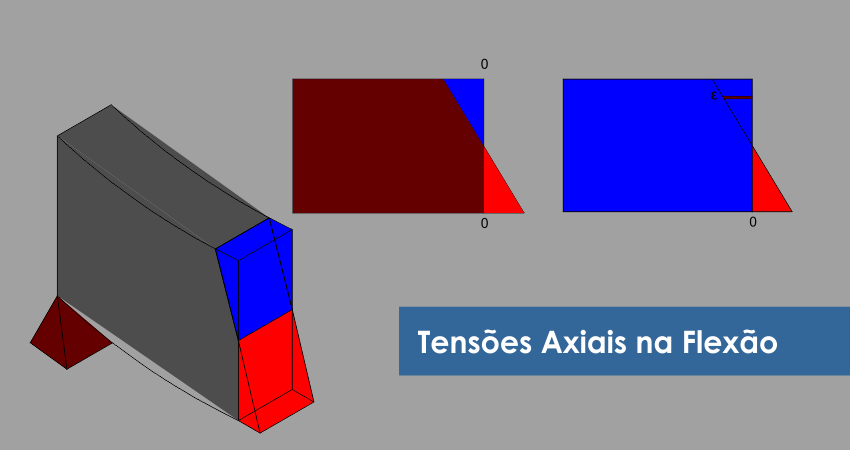
Há de se lembrar, como mostra a figura 5, que as transmissões de tensão são simétricas enquanto o concreto estiver no seu regime linear elástico. A tabela 1 mostra os valores de fctk para algumas resistências de concreto.

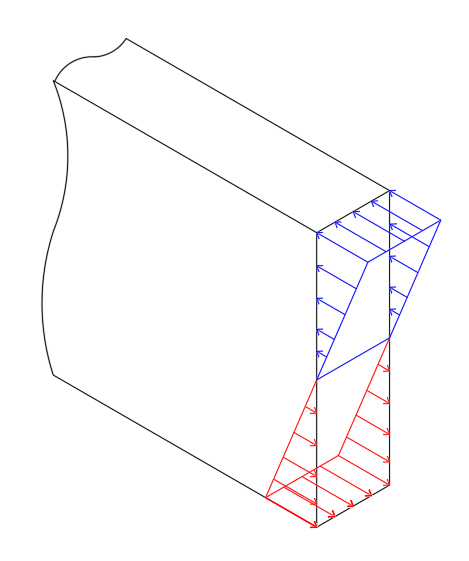
Figura 5 – Tensões simétricas lineares e elásticas em uma seção de viga

Tabela 1 – Valores de fck e fctk calculados para concretos de resistência normal (Valores em MPa)

Após fissurado, o concreto não é mais considerado resistente e todos os esforços de tração da seção são resistidos pelo aço. Repare que os valores de 0,5fck são sempre maiores do que os valores de fctk. Isso quer dizer que, mesmo após fissurado, o concreto à tração, o concreto a compressão ainda está em seu estado elástico, então, existe ainda valore de tensão a serem alcançados antes da plastificação do concreto. Portanto, a segunda mudança física na seção ocorre quando o concreto inicia sua plastificação e assim segue até a ruptura.

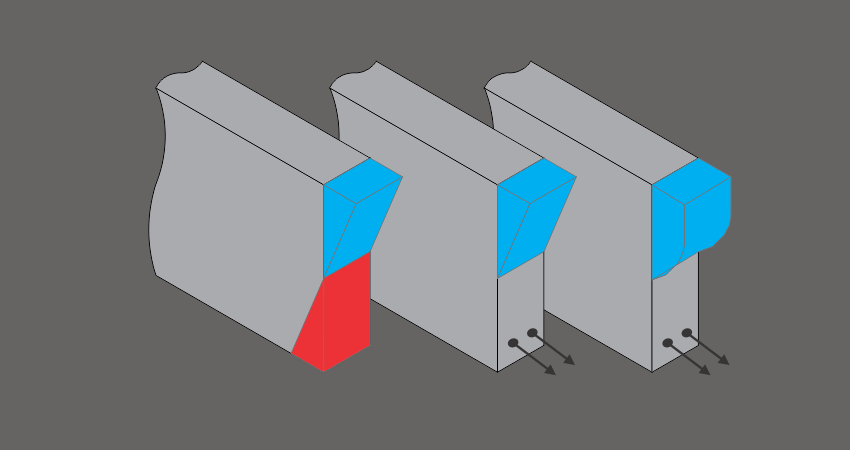
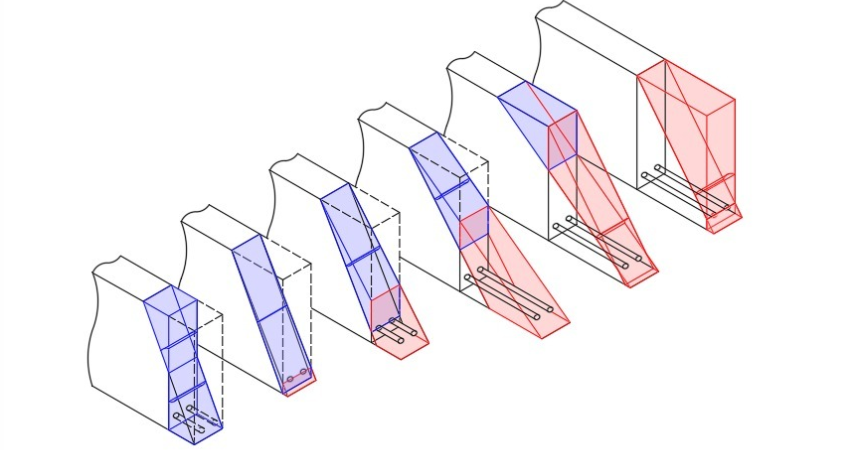
A cada alteração física das tensões na seção dá-se o nome de Estádio. O primeiro estádio de tensão é configurado pelo estado elástico total do concreto (Estádio I). No Segundo estádio temos a seção fissurada, o aço agindo à tração, e o concreto ainda em sua fase elástica à compressão (Estádio II). E o terceiro e último estádio é configurado pela plastificação do concreto à compressão, maior fissuração à tração e o aço agindo à tração.

Uma outra observação é importante! Vamos relembrar a equação das tensões elásticas em uma viga qualquer em regime elástico como consta na equação 8:

Se isolarmos os momentos, podemos encontrar com facilidade os momentos fletores limites em que a viga muda de estádio. A equação 9 guiará nosso cálculo!

Assim, Sabendo que o Estádio I inicia exatamente após o concreto atingir seu momento de fissuração (σ=fctk) o momento limite do Estádio I é obtido a partir da equação 10.

Eq. 10.

O Estádio II ocorre quando o concreto atinge seu limite elástico (σ=0,5fck). A equação 11 monta a equação limite do Estádio II.

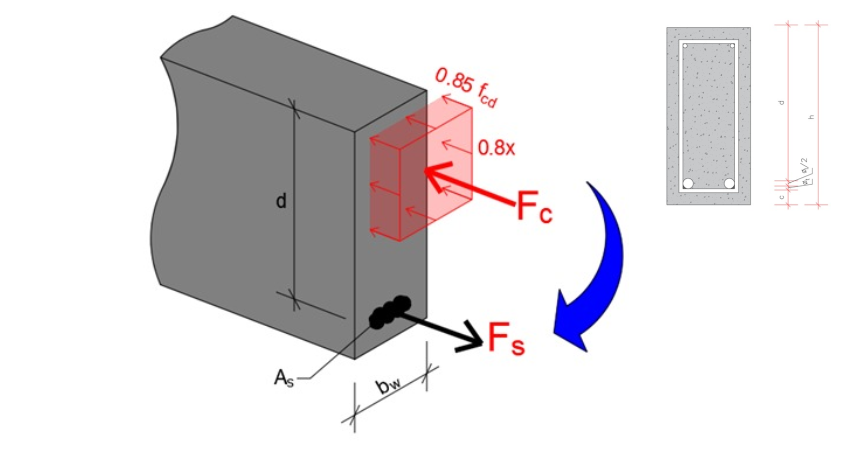
Para o Estádio III, a equação 9 não vale, pois não estamos mais sob o regime elástico. Então, a linha neutra não encontra-se à meia altura da seção. Obtemos a linha neutra segundo a equação 12.

Assim sendo, todas as seções cujos momentos ultrapassarem os momentos limites do Estádio II estarão no estádio III. Sabendo que uma viga tem infinitas seções, e por exemplo, biapoiada com carregamento uniformemente distribuído (figura 6a) terá o diagrama como mostrado na figura 6b, Todas as seções compreendidas com momentos fletores menores que os respectivos limites, estará no Estádio respectivo como mostra a figura 6c (em vermelho, Estádio II, em Verde Estádio II, em azul, Estádio III). Cada estádio terá as tensões distribuídas segundo a figura 7 sendo o Estádio I conforme mostra a figura 7ª, A Figura 7b mostra o Estádio II e o Estádio III é mostrado na figura 7c.

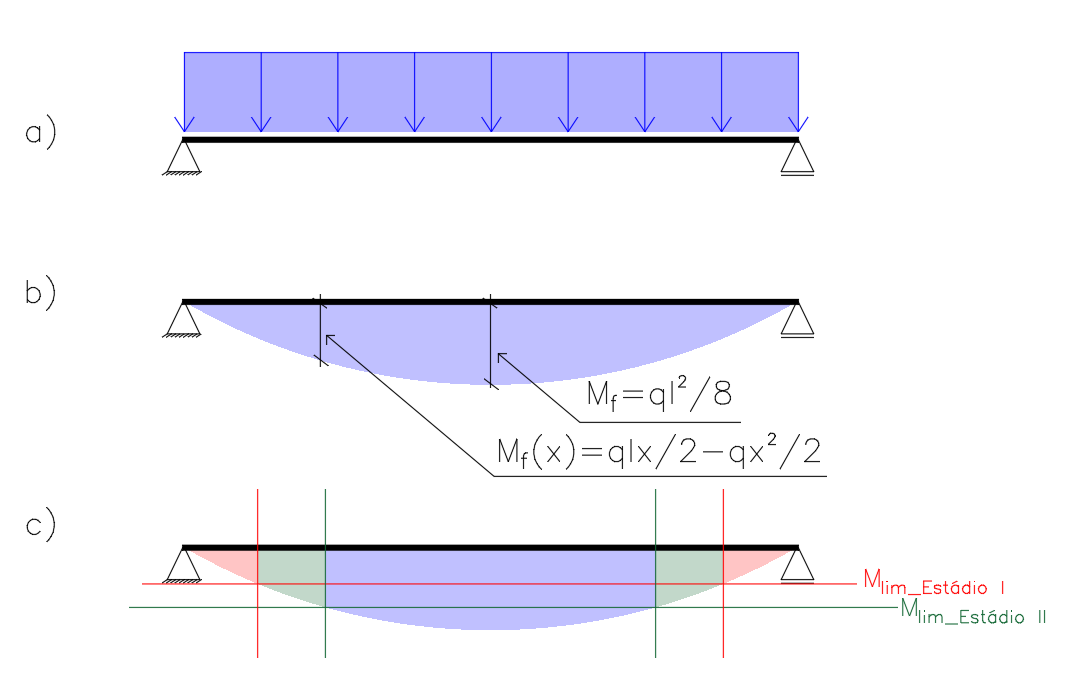
Figura 6 – Diagramas da viga-exemplo

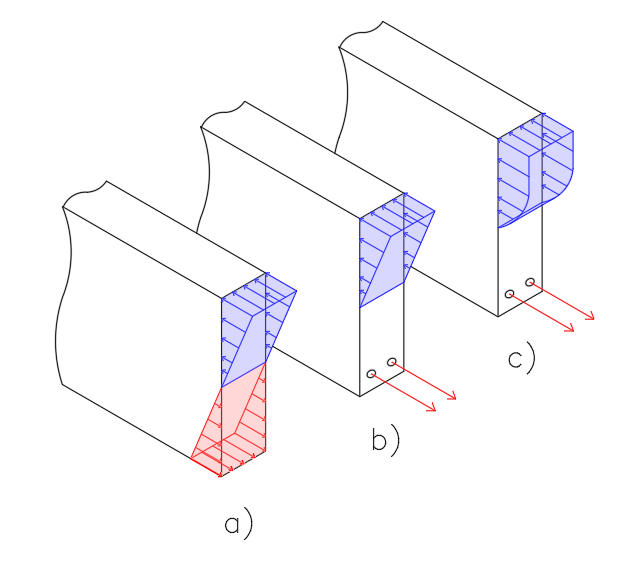
Figura 7 – Estádios de Tensão