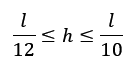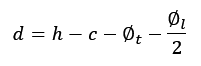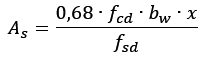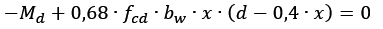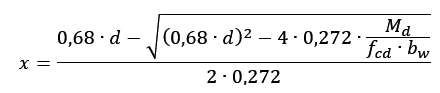Depois de um período longe, voltei!
Vamos falar um pouco sobre dimensionamento!!!! E após isso, na próxima publicação, sobre os aspectos desse dimensionamento, as escolhas a serem feitas antes de dimensionar e os limites impostos a esse dimensionamento. Portanto, as equações aqui mostradas resolvem apenas 1 tipo de elemento e, ainda, não consta neste artigo todo o conhecimento necessário para que seja totalmente compreendido. No entanto, simplifica bastante a forma de apresentar ao leitor como funciona o concreto armado. Observem que não sigo a lógica comum dos livros, mas, o blog tratará de tudo o que o livro trata em uma ordem que julgo mais compreensível. Vamos falar, dessa vez, sobre as vigas retangulares simplesmente armadas (ou seja, com armadura resistente apenas à tração).

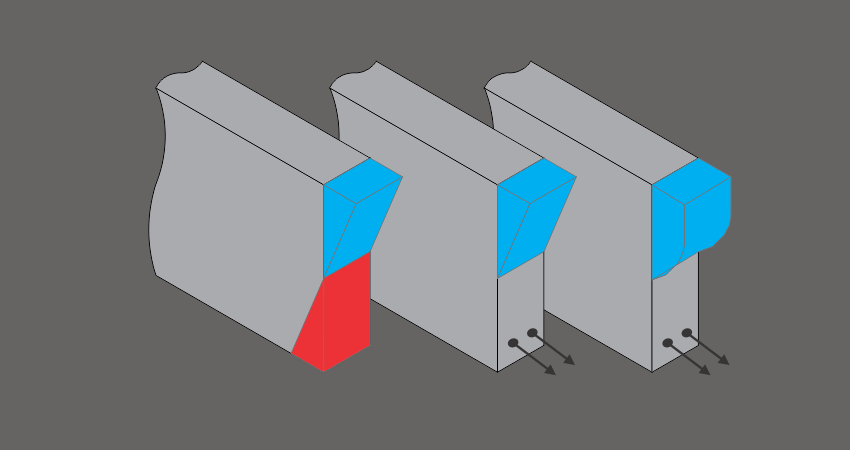
Essas vigas são dimensionadas com área de aço resistente em apenas uma de suas bases. Em momentos positivos, a armadura resistente é posicionada apenas na base inferior da viga. Em momentos negativos, a armadura é posicionada na base superior das vigas. Em todos os casos, a posição dessa armadura é importante de ser conhecida. A figura 1 mostra partes da viga.

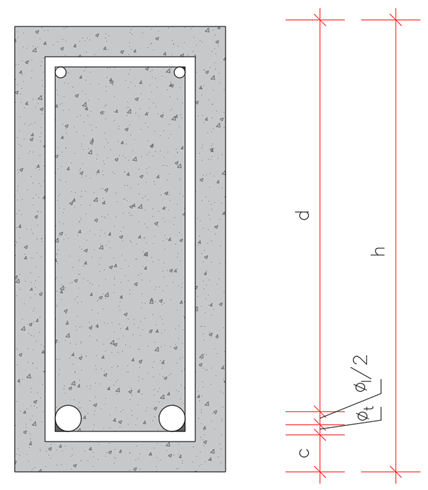
Figura 1 – Seção de viga

A partir das cotas da figura 1, podemos deduzir a forma de obtenção do valor da altura útil da viga a partir de uma altura predeterminada (normalmente por pré-dimensionamento como mostrado na Equação 1 que apresenta uma forma prática de determinar uma altura inicial para o dimensionamento de vigas em obras usuais). A Equação 2 coloca a forma de obtenção da altura útil inicial para o dimensionamento considerando uma seção de barra de aço escolhida previamente.

Sendo:

l – Vão da viga

d – altura útil

c – cobrimento da armadura conforme a NBR 6118/2014

∅t – o diâmetro do estribo

∅l – o diâmetro da armadura longitudinal (de flexão)

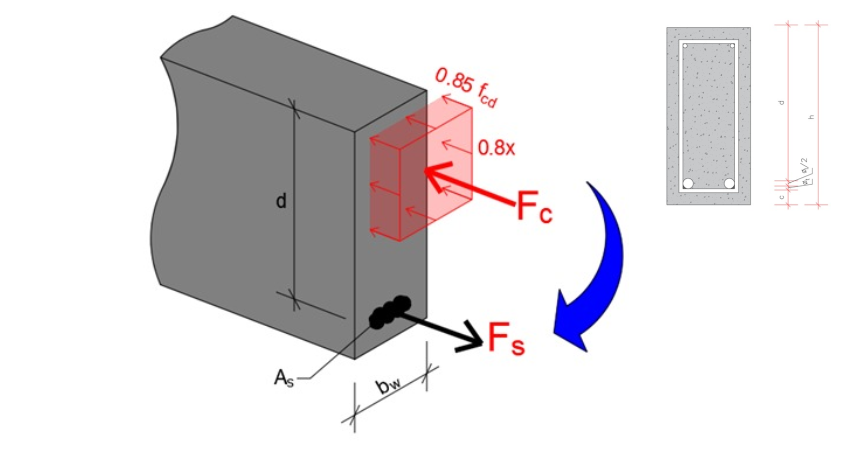
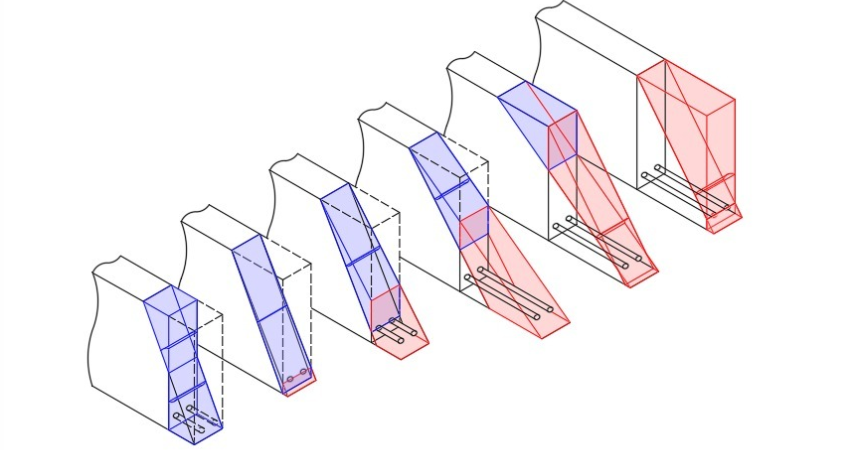
O funcionamento mecânico da seção de concreto armado ocorre conforme mostra a figura 2.  Há de se pontuar que o diagrama retangular simplificado orientado pela NBR 6118 será utilizado. Em aula, comprovaremos que ele é, sim, conveniente. Entretanto, na realidade a seção deveria ser calculada conforme a diagrama parábola-retângulo, mas, como o diagrama tensão-deformação do concreto é um conjunto combinado de duas formas, sendo uma delas curva, precisaríamos recorrer a integrais desnecessariamente trabalhosas.

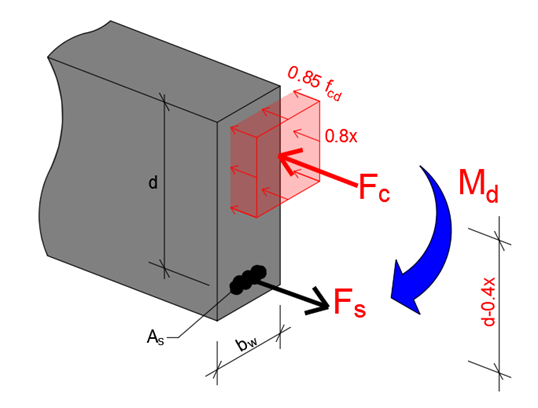
Figura 2 – Diagramas de Forças atuantes simplificadas na seção de concreto armado

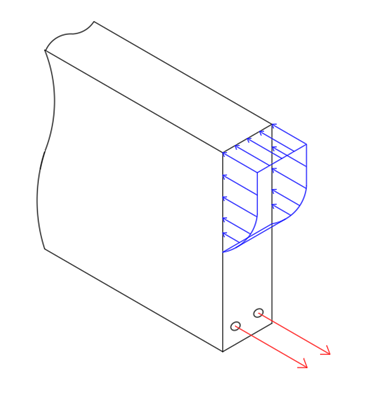
Figura 3 – Diagramas de forças não-simplificados na seção de concreto armado.

Como dito previamente, as estruturas de concreto armado são adaptações de teorias advindas da resistência dos materiais. Portanto, sabendo que isso para a figura 2, basta que recorramos a uma das leis da estática: Somatório das forças igual a zero.

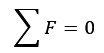
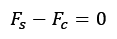
Tal que aplicando a equação das tensões de Pascal e isolando a força:

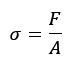
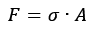
Aplicando isso ao aço e concreto:

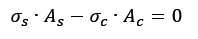
Sabendo que as tensões no aço e no concreto são as tensões ponderadas fsd e fcd além de a tensão minorada do concreto sofrer uma minoração do coeficiente Rüsch tornando-se 0,85fcd.

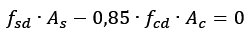
A área de concreto comprimida, então, observando na figura 2 corresponde à bw⋅0,8x.

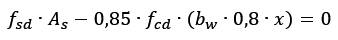
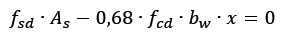
Se o que desejamos obter é a área de aço, isolaremos esta no lado esquerdo da equação, obtendo a equação 3.

Apesar de termos já a equação para obtenção da área de aço, é preciso observar que temos outra incógnita envolvida. Não sabemos qual é a altura da linha neutra ainda. Mas, se bem lembrarmos dos princípios da estática, ainda resta uma equação de equilíbrio a ser trabalhada: Somatório dos momentos é igual a zero em qualquer ponto da seção. Utilizaremos o centro de gravidade da armadura, por conveniência, já que a distância entre o centro de gravidade da armadura e a posição de aplicação da sua carga é zero, isso anula seu momento nesse ponto e elimina da equação a incógnita Área de Aço. (consideremos anti-horário positivo).

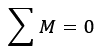
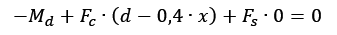
Simplificando:

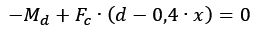
Fazendo agora a substituição da tensão no concreto e da Área comprimida como feito previamente:

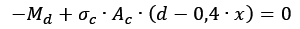
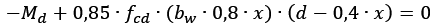
Assim, chegamos a equação 4.

Executando as demais multiplicações:

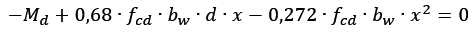
Dividindo todos os membros por fcd‧bw:

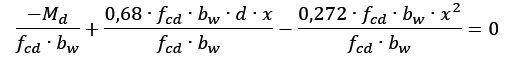
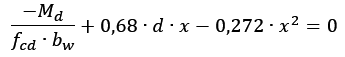
Reorganizando a equação:

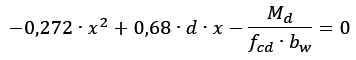
Agora, fazendo um esquema de cores:

Fica fácil perceber que a última equação pode ser comparada com a equação de segundo grau.

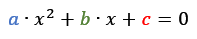
Onde:

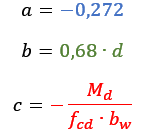
Resolvendo por Báskhara, obtemos a equação 5:

Tendo em mãos o valor da linha neutra, encontramos com facilidade a área de aço. E está resolvida a viga retangular simplesmente armada.